题目内容
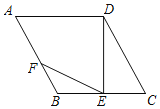
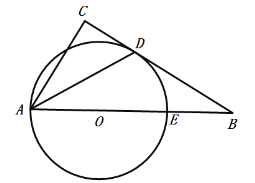
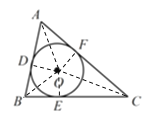
【题目】如图所示，
分别切
的三边
、
、
于点
、
、
，若
，
，
．
（1）求
的长；
（2）求的半径长．
【答案】（1）4；（2）2
【解析】
（1）设AD=x，根据切线长定理得到AF=AD,BE=BD,CE=CF,根据关系式列得方程解答即可；
（2）连接OD、OE、OF、OA、OB、OC，将△ABC分为三个三角形：△AOB、△BOC、△AOC，再用面积法求得半径即可.
解：（1）设 
，
分别切 
的三边 
、
、
于点 
、
、
，
，
，
，
，
，
，
，
即 
，得 
，
的长为 
．
（2）如图，连接OD、OE、OF、OA、OB、OC，
则OD⊥AB,OE⊥BC,OF⊥AC,且OD=OE=OF=2，
∵
，，,
∴AB2+BC2=AC2，
∴△ABC是直角三角形，且∠B是直角，
,∴
,
∴OD=2,即
的半径长为2.
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
