题目内容
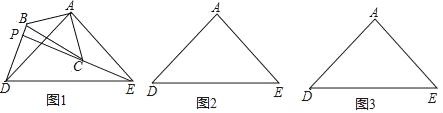
【题目】如图,已知:在△ABC中,AB、BC边上的垂直平分线相交于点P.若∠BAC=50°,则∠BPC的度数为( )
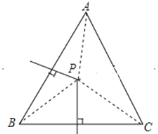
A.100°B.110°C.115°D.120°
【答案】A
【解析】
根据垂直平分线的性质得到AP=BP=CP,从而有∠1=∠3,∠2=∠5,则∠3+∠5=∠1+∠2=50°,于是有∠3+∠5+∠4+∠6=180°-50°=130°,从而可得到∠4+∠6,然后根据三角形的内角和定理即可计算出∠BPC的度数.
解:∵AB、BC的垂直平分线相交于点P,
∴AP=BP=CP,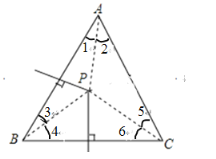
∴∠1=∠3,∠2=∠5,
而∠BAC=50°,
∴∠3+∠5=∠1+∠2=50°,
而∠3+∠4+∠5+∠6=180°-50°=130°,
∴∠4+∠6=130°-50°=80°,
∴∠BPC=180°-∠4-∠6=100°.
故选:A.

练习册系列答案
相关题目