题目内容
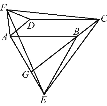
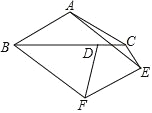
【题目】如图,在等腰△ABC 中,∠BAC=120°,AB=AC=2![]() ,点 D 在边 BC 上,CD=
,点 D 在边 BC 上,CD=![]() ,将线段 CD 绕点 C 逆时针旋转α°(其中 0<α≤360)到 CE,连接AE,以 AB,AE 为边作 ABFE,连接 DF,则 DF 的最大值为( )
,将线段 CD 绕点 C 逆时针旋转α°(其中 0<α≤360)到 CE,连接AE,以 AB,AE 为边作 ABFE,连接 DF,则 DF 的最大值为( )
A. ![]() +
+![]() B.
B. ![]() +
+![]() C. 2
C. 2![]() +
+![]() D.
D. ![]() +2
+2![]()
【答案】B
【解析】
作平行四边形 ABPC,连接 PA 交 BC 于点 O,连接 PF.解直角三角形求得 PD=![]() ,由四边形 PCEF 是平行四边形,推出 PF=EC=
,由四边形 PCEF 是平行四边形,推出 PF=EC=![]() ,推出点
,推出点
F 的运动轨迹是以 P 为圆心![]() 为半径的圆,由此即可解决问题.
为半径的圆,由此即可解决问题.
作平行四边形 ABPC,连接 PA 交 BC 于点 O,连接 PF.
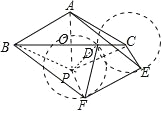
∵四边形 ABPC 是平行四边形,AB=BC,
∴四边形 ABPC 是菱形,
∴PA⊥BC,
∵AB=AC=2![]() ,∠ABC=120°,
,∠ABC=120°,
∴∠BAO=60°,
∴OA=OP=![]() ,OB=OC=3
,OB=OC=3![]() ,
,
∵CD=![]() ,
,
∴OD=2![]() ,
,
∴PD= ![]() =
=![]() ,
,
∵AB∥PC∥PE,AB=PC=EF,
∴四边形 PCEF 是平行四边形,
∴PF=CE=CD=![]() ,
,
∴点 F 的运动轨迹是以 P 为圆心![]() 为半径的圆,
为半径的圆,
∴DF 的最大值![]() 故答案选:B.
故答案选:B.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目