题目内容
【题目】已知:如图,在□ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,过点F作FG⊥BF交BC的延长线于点G.
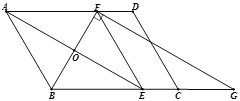
(1)求证:四边形ABEF是菱形;
(2)如果AB= 2,∠BAD=60°,求FG的长.
【答案】(1)见解析;(2) ![]()
【解析】
(1)根据平行四边形的性质证得AB=BE=AF,得到四边形ABEF是平行四边形,再根据邻边相等证得结论;
(2)根据菱形的性质求得∠BAE=30°,OB=OF=1,再根据FG⊥BF求出∠G==30°,得到BG=4,根据勾股定理求出FG.
(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠DAE=∠BAE.
∴∠AEB =∠BAE.
∴AB=BE.
同理:AB=AF.
∴AF=BE,AF∥BE,
∴四边形ABEF是平行四边形.
又∵AB=BE,
∴四边形ABEF是菱形.
(2) ∵四边形ABEF是菱形,
∴AE⊥BF,OA=OE,OB=OF,AE平分∠BAD,
∵AB= 2,∠BAD=60°,
∴∠BAE=30°,∠FBE=∠ABF=60°,
∴OB=OF=1,
∴BF=2,
又∵FG⊥BF,
∴∠BFG==90°,
∴∠G==30°,
∴BG=4,
∴![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】在数学课上,老师出了这样一道题:甲、乙两地相距1400km,乘高铁列车从甲地到乙地比乘特快列车少用9h,已知高铁列车的平均行驶速度是特快列车的2.8倍.求高铁列车从甲地到乙地的时间.
老师要求同学先用列表方式分析再解答.下面是两个小组分析时所列的表格:
小组甲:设特快列车的平均速度为![]() km/h.
km/h.
时间/h | 平均速度/(km/h) | 路程/km | |
高铁列车 | 1400 | ||
特快列车 |
| 1400 |
小组乙:高铁列车从甲地到乙地的时间为![]() h.
h.
时间/h | 平均速度/(km/h) | 路程/km | |
高铁列车 |
| 1400 | |
特快列车 | 1400 |
(1)根据题意,填写表格中空缺的量;
(2)结合表格,选择一种方法进行解答.