题目内容
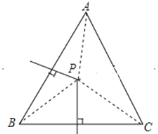
【题目】在△ABC 中,∠ABC=60°,BC=8,点 D 是 BC 边的中点,点 E 是边 AC上一点,过点 D 作 ED 的垂线交边 AC 于点 F,若 AC=7CF,且 DE 恰好平分△ABC 的周长,则△ABC 的面积为______.
【答案】10
【解析】
取 AC 的中点 M,连接 DM,作 AH⊥BC 于 H.设 DM=a,AE=b.想办法证明 DM=EM=FM=a.AE=CF=b,2a=5b,解直角三角形求出 BH,CH 用 b 表示,根据边长的长构建方程求出 b 即可解决问题;
如图,取AC的中点M,连接DM,作AH⊥BC于H.

设 DM=a,AE=b.
∵BD=DC,AM=MC,
∴AB=2DM=2a,
∵AB+AE+BD=EC+DC,
∴EC=2a+b,AC=2a+2b,
∴AM=MC=a+b,
∴EM=a,
∴EM=DM,
∴∠MED=∠MDE,
∵∠MED+∠MFD=90°,∠MDE+∠MDF=90°,
∴∠MFD=∠MDF,
∴MD=MF=a,
∴CF=AE=b,
∵AC=7CF,
∴2a+2b=7b,
∴2a=5b,
∵AB=5b,AC=7b,
在 Rt△ABH 中,∵∠B=60°,
∴BH= ![]() AB=
AB= ![]() b,AH=
b,AH= ![]() b,
b,
在 Rt△ACH 中,CH=![]() =
=![]() b,
b,
∴BC=BH+HC=8b,
∴8b=8,
∴b=1,
∴S△ABC= ![]() ×8×
×8×![]() =10
=10![]() ,
,
故答案为: 10![]() .
.

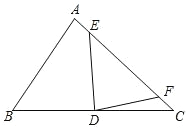
【题目】如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C.
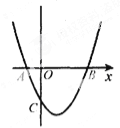
(1)点A的坐标为 点B的坐标为 ,点C的坐标为 ;
(2)设抛物线y=x2-2x-3的顶点坐标为M,求四边形ABMC的面积.
【题目】(8分)某中学数学活动小组为了调查居民的用水情况,从某社区的![]() 户家庭中随机抽取了
户家庭中随机抽取了![]() 户家庭的月用水量,结果如下表所示:
户家庭的月用水量,结果如下表所示:
月用水量(吨) |
|
|
|
|
|
|
|
户数 |
|
|
|
|
|
|
|
(1)求这![]() 户家庭月用水量的平均数、众数和中位数;
户家庭月用水量的平均数、众数和中位数;
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的办法引导人们节约用水,即规定每个家庭的月基本用水量为![]() (吨),家庭月用水量不超过
(吨),家庭月用水量不超过![]() (吨)的部分按原价收费,超过
(吨)的部分按原价收费,超过![]() (吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合理?简述理由.
(吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合理?简述理由.
【题目】如图,一个滑道由滑坡(AB段)和缓冲带(BC段)组成,滑雪者在滑坡上滑行的距离y1(单位:m)和滑行时间t1(单位s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s.
(1)求y1和t1满足的二次函数解析式;
(2)求滑坡AB的长度.
【题目】在数学课上,老师出了这样一道题:甲、乙两地相距1400km,乘高铁列车从甲地到乙地比乘特快列车少用9h,已知高铁列车的平均行驶速度是特快列车的2.8倍.求高铁列车从甲地到乙地的时间.
老师要求同学先用列表方式分析再解答.下面是两个小组分析时所列的表格:
小组甲:设特快列车的平均速度为![]() km/h.
km/h.
时间/h | 平均速度/(km/h) | 路程/km | |
高铁列车 | 1400 | ||
特快列车 |
| 1400 |
小组乙:高铁列车从甲地到乙地的时间为![]() h.
h.
时间/h | 平均速度/(km/h) | 路程/km | |
高铁列车 |
| 1400 | |
特快列车 | 1400 |
(1)根据题意,填写表格中空缺的量;
(2)结合表格,选择一种方法进行解答.