题目内容
【题目】在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE , 现给出下列命题正确的是( )
①若 ![]() ,则
,则 ![]() ;
;
②若DE2=BDEF,则DF=2AD.
A.①是真命题,②是真命题
B.①是真命题,②是假命题
C.①是假命题,②是真命题
D.①是假命题,②是假命题
【答案】A
【解析】解:①设CF=x,DF=y,BC=h,则由已知菱形BFDE,BF=DF=y
由已知得: ![]() =
= ![]() ,
,
得: ![]() =
= ![]() ,即cos∠BFC=
,即cos∠BFC= ![]() ,
,
∴∠BFC=30°,
由已知
∴∠EDF=30°
∴tan∠EDF= ![]() ,
,
所以①是真命题.
②已知菱形BFDE,∴DF=DE
S△DEF= ![]() DFAD=
DFAD= ![]() BDEF,
BDEF,
又DE2=BDEF(已知),
∴S△DEF= ![]() DE2=
DE2= ![]() DF2 ,
DF2 ,
∴DFAD= ![]() DF2 ,
DF2 ,
∴DF=2AD,
∴②是真命题.
故选:A.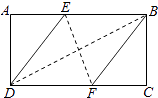
【考点精析】关于本题考查的菱形的性质和矩形的性质,需要了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某校对七、八、九年级的学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
各年级学生成绩统计表 | 优秀 | 良好 | 合格 | 不合格 |
七年级 | a | 20 | 24 | 8 |
八年级 | 29 | 13 | 13 | 5 |
九年级 | 24 | b | 14 | 7 |
根据以上信息解决下列问题:
(1)在统计表中,a的值为 , b的值为;
(2)在扇形统计图中,八年级所对应的扇形圆心角为度;
(3)若该校三个年级共有2000名学生参加考试,试估计该校学生体育成绩不合格的人数.