题目内容
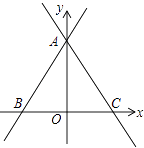
【题目】如图(1),PT与⊙O1相切于点T,PAB与⊙O1相交于A、B两点,可证明△PTA∽△PBT,从而有PT2=PAPB.请应用以上结论解决下列问题:如图(2),PAB、PCD分别与⊙O2相交于A、B、C、D四点,已知PA=2,PB=7,PC=3,则CD= . 
【答案】![]()
【解析】解:如图2中,过点P作⊙O的切线PT,切点是T. 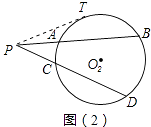
∵PT2=PAPB=PCPD,
∵PA=2,PB=7,PC=3,
∴2×7=3×PD,
∴PD= ![]()
∴CD=PD﹣PC= ![]() ﹣3=
﹣3= ![]() .
.
如图2中,过点P作⊙O的切线PT,切点是T,根据PT2=PAPB=PCPD,求出PD即可解决问题.本题考查相似三角形的判定和性质、切线的性质等知识,解题的关键是理解题意,学会利用新知解决未知,属于中考常考题型.

【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |

(1)频数分布表中a= , b= , 并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?
【题目】如图,某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1000名学生中,随机抽取了若干名学生进行调查,了解学生最喜欢的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
球类名称 | 乒乓球 | 排球 | 羽毛球 | 足球 | 篮球 |
人数 | a | 12 | 36 | 18 | b |

解答下列问题:
(1)本次调查中的样本容量是;
(2)a= , b=;
(3)试估计上述1000名学生中最喜欢羽毛球运动的人数.