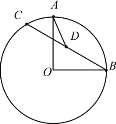
题目内容
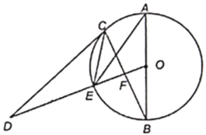
【题目】如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.以点D为圆心,适当长为半径画弧,交DA于点G,交DC于点H.再分别以点G、H为圆心,大于![]() GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则△ADF的形状是( )
GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则△ADF的形状是( )
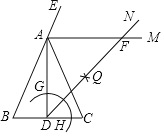
A.等腰三角形B.等边三角形
C.直角三角形D.等腰直角三角形
【答案】D
【解析】
根据画图过程可得:DF平分∠ADC,∠ADF=∠CDF,根据AB=AC,得∠B=∠ACB,由AM是△ABC外角∠CAE的平分线,证得∠EAF=∠B,得AF∥BC,进而证明△ADF的形状.
解:根据画图过程可知:
DF平分∠ADC,
∴∠ADF=∠CDF,
∵AB=AC,
∴∠B=∠ACB,
∵AM是△ABC外角∠CAE的平分线,
∴∠EAM=∠CAM,
∵∠EAC=∠B+∠ACB,
∴∠EAF=∠B,
∴AF∥BC,
∴∠AFD=∠FDC,
∴∠AFD=∠ADF,
∴AF=AD,
∵AD是高,
∴∠ADB=90°,
∴∠FAD=∠ADB=90°,
∴△ADF的形状是等腰直角三角形.
故选:D.

 全优点练单元计划系列答案
全优点练单元计划系列答案【题目】在“新冠肺炎防控”知识宣传活动中,某社区对居民掌握新冠肺炎防控知识的情况进行调查.其中![]() 、
、![]() 两区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
两区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
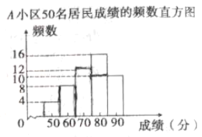
(信息一)![]() 小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
(信息二)图中,![]() 小区从左往右第四组的成绩如下
小区从左往右第四组的成绩如下
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() 、
、![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | 79 |
| 277 | |
| 75.1 | 77 | 76 |
| 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数;
小区50名居民成绩的中位数;
(2)请估计![]() 小区500名居民中能超过平均数的有多少人?
小区500名居民中能超过平均数的有多少人?
(3)请尽量从多个角度比较、分析![]() ,
,![]() 两小区居民掌握新冠防控知识的情况.
两小区居民掌握新冠防控知识的情况.
【题目】阅读对学生的成长有着深远的影响.某中学为了解学生每周课余阅读的时间,在本校随机抽取若干名学生进行调查,并依据调查结果经制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A |
| 6 |
|
B |
|
|
|
C |
| 10 |
|
D |
| 8 |
|
E |
| 4 |
|
合计 | 1 |
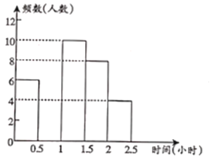
请根据图表中的信息,解答下列问题:
(1)表中的![]() ,
,![]() ,将频数分布直方图补全;
,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足1小时的学生大约有多少名?
(3)![]() 组的4人中,有1名男生和3名女生,该校计划在
组的4人中,有1名男生和3名女生,该校计划在![]() 组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.
组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.