题目内容
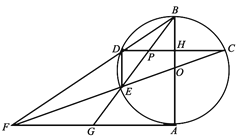
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是圆上一点,
是圆上一点,![]() ,垂足为点
,垂足为点![]() ,
,![]() 交
交![]() 于点
于点![]() ,且
,且![]() .
.
(1)若点![]() 是
是![]() 的中点,求证:
的中点,求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() 的半径为10,
的半径为10,![]() ,求
,求![]() 的值.
的值.
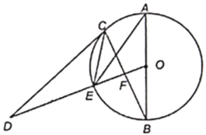
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)利用SAS证明△BOF≌△CEF即可证得CE=BO;
(2)先证明∠OCB=∠D,因为∠DCF+∠D=90°,所以∠DCF+∠OCB=90°即CD⊥CD,因为OC是⊙O的半径,所以CD是⊙O的切线
(3)在Rt△OCF中,已知OC=10,可求得![]() ,根据勾股定理OF=6
,根据勾股定理OF=6
证明Rt△OFC∽Rt△OCD,得出![]() ,即可求出OD,进而求出DE,即可求出
,即可求出OD,进而求出DE,即可求出![]() .
.
(1)∵OD⊥BC,OE是⊙O的半径
∴∠BFO=∠CFE=90°,BF=CF
∵F是OE的中点
∴EF=OF
在△BOF和△CEF中

∴△BOF≌△CEF(SAS)
∴CE=BO
(2)如图,连接OC

∵OB=OC
∴∠OCB=∠B
∵∠B=∠AEC,∠D=∠AEC
∴∠B=∠D
∴∠OCB=∠D
∵OD⊥BC
∴∠DCF+∠D=90°
∴∠DCF+∠OCB=90°即∠OCD=90°
∴CD⊥CD
∵OC是⊙O的半径
∴CD是⊙O的切线
(3)在Rt△OCF中,OC=10
∵OD⊥BC,OE是⊙O的半径
∴![]()
∴在Rt△OCF中,![]()
∵∠COF=∠DOC,∠OFC=∠OCD=90°
∴Rt△OFC∽Rt△OCD
∴![]() 即
即![]()
∴![]()
∴![]()
∴
故答案为:![]()

练习册系列答案
相关题目