题目内容
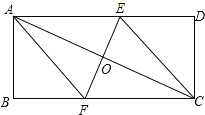
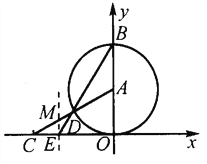
【题目】如图,将一个直角三角形纸片![]() ,放置在平面直角坐标系中,点
,放置在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() .将
.将![]() 沿
沿![]() 翻折得到
翻折得到![]() (点
(点![]() 为点
为点![]() 的对应点).
的对应点).
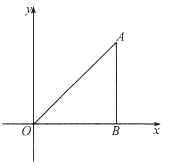
(Ⅰ)求![]() 的长及点
的长及点![]() 的坐标;
的坐标;
(Ⅱ)点![]() 是线段
是线段![]() 上的点,点
上的点,点![]() 是线段
是线段![]() 上的点.
上的点.
①已知![]() ,
,![]() ,
,![]() 是
是![]() 轴上的动点,当
轴上的动点,当![]() 取最小值时,求出点
取最小值时,求出点![]() 的坐标及点
的坐标及点![]() 到直线
到直线![]() 的距离;
的距离;
②连接![]() ,
,![]() ,且
,且![]() ,现将
,现将![]() 沿
沿![]() 翻折得到
翻折得到![]() (点
(点![]() 为点
为点![]() 的对应点),再将
的对应点),再将![]() 绕点
绕点![]() 顺时针旋转,旋转过程中,射线
顺时针旋转,旋转过程中,射线![]() ,
,![]() 交直线
交直线![]() 分别为点
分别为点![]() ,
,![]() ,最后将
,最后将![]() 沿
沿![]() 翻折得到
翻折得到![]() (点
(点![]() 为点
为点![]() 的对应点),连接
的对应点),连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
【答案】(Ⅰ)![]() ,
,![]() 点坐标为
点坐标为![]() ;(Ⅱ)①点
;(Ⅱ)①点![]() 的坐标为
的坐标为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;②
;②![]() 或
或![]() 或
或![]() .
.
【解析】
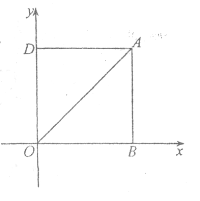
(Ⅰ)根据A点坐标和翻折的性质可得四边形OBAD为正方形,即可得出D点坐标,再利用勾股定理得出OA的长.
(Ⅱ)①作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 与
与![]() 轴交于点
轴交于点![]() ,则点
,则点![]() 即为所求,再根据待定系数法确定直线
即为所求,再根据待定系数法确定直线![]() 的解析式,求出直线
的解析式,求出直线![]() 与x轴的交点
与x轴的交点![]() 的坐标,再根据等积法求出点
的坐标,再根据等积法求出点![]() 到直线
到直线![]() 的距离即可.
的距离即可.
②分(a)当点M在线段EA的延长线上,点N在线段AE时,(b)当点M,N在线段EA上时,(c)当点M在线段EA上,点N在AE的延长线上时,三种情况进行讨论,作MH⊥OB于H,GK⊥EB于K,然后证明△AMH≌△GAK,推出HM=EH=BK,BH=GK,所以BH=EK=GK,从而得出∠MEG=90°,由NE:EG=5:12,设NE=5k,EG=12k,则MN=NG=13k,EM=18k,可得BH=GK=EK=6![]() k,EH=MH=9
k,EH=MH=9![]() k,再根据HE=AH+AE,得出关于k的方程,得出k的值即可解决问题;
k,再根据HE=AH+AE,得出关于k的方程,得出k的值即可解决问题;
解:(Ⅰ)如图,∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
∵![]() ,
,
∴![]() .
.
∵将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,
,
∴![]() .
.
∴![]()
∴点![]() 落在
落在![]() 轴上.
轴上.![]() 点坐标为
点坐标为![]() .
.
(Ⅱ)①如图,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,若在
,若在![]() 轴上任取点
轴上任取点![]() (与点
(与点![]() 不重合).连接
不重合).连接![]() ,
,![]() ,
,![]() ,
,
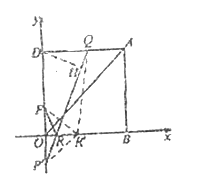
由![]() ,
,
可知![]() 最小.
最小.
∵将![]() 沿
沿![]() 翻折得到
翻折得到![]() .
.
∴![]() ,
,![]()
∵![]() ,
,
![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
设直线![]() 的方程为
的方程为![]() .
.
将![]() 的坐标代入,
的坐标代入,
得![]() ,
,
解得![]() .
.
∴直线![]() 的方程为
的方程为![]()
当![]() 时,
时,![]() ,
,
∴当![]() 取最小值时,点
取最小值时,点![]() 的坐标为
的坐标为![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
∴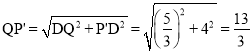 .
.
过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
∵![]() ,
,
∴
∴当![]() 取最小值时,点
取最小值时,点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
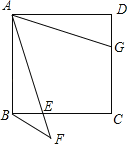
②(a)如图3中,当点M在线段EA的延长线上,点N在线段AE时,
作MH⊥OB于H,GK⊥EB于K,
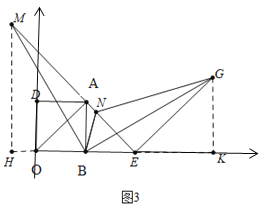
由翻折可知:∠MBN=∠NBG=45°,BM=BG,
∴∠MBG=90°,
∵∠MHB=∠K=90°,
∴∠MBH+∠GBK=90°,∠HBM+∠BMH=90°,
∴∠BMH=∠GBK,
∴△BMH≌△GBK,
∴HM=EH=BK,BH=GK,
∴BH=EK=GK,
∴∠GEK=∠BEA=45°,
∴∠MEG=90°,
∵NE:EG=5:12,设NE=5k,EG=12k,则MN=NG=13k,EM=18k,
∴BH=GK=EK=6![]() k,EH=MH=9
k,EH=MH=9![]() k,
k,
∵HE=BH+BE,
∴9![]() k=6
k=6![]() k+3,
k+3,
∴k=![]() ,∴EH=MH=9,
,∴EH=MH=9,
∴OH=3.∴点![]() 的坐标为
的坐标为![]()
(b)如图4中,当点M,N在线段EA上时,同法可得:点![]() 的坐标为
的坐标为![]() .
.
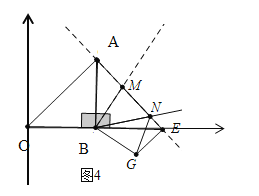
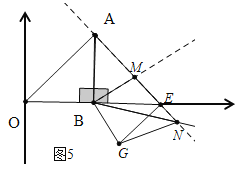
(c)如图5中,当点M在线段EA上,点N在AE的延长线上时,同法可得:点![]() 的坐标为
的坐标为![]() .
.
综上所述,点![]() 的坐标
的坐标![]() 或
或![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案