题目内容
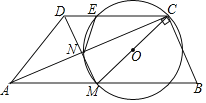
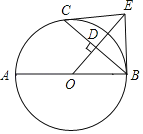
【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连结BE.
(1)求证:BE与⊙O相切;
(2)若OD=DE,AB=6,求由![]() ,线段BC,AB所围成图形的面积.
,线段BC,AB所围成图形的面积.
【答案】(1)详见解析;(2)![]() π+
π+![]() .
.
【解析】
(1)连接OC,易证得△COE≌△BOE(SAS),即可得∠OCE=∠OBE=90°,证得BE与⊙O相切;
(2)根据切线的性质得到CE=BE,推出四边形OBEC是正方形,得到∠BOC=90°,根据平角的定义得到∠AOC=90°,根据扇形和三角形的面积公式即可得到结论.
(1)证明:连接OC,
∵CE是⊙O的切线,
∵OB=OC,OD⊥BC,
∴∠EOC=∠EOB,
∵在△EOC和△EOB中,,
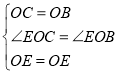
∴△COE≌△BOE(SAS),
∴∠OCE=∠OBE=90°,
即OB⊥BE,
∴BE与⊙O相切;
(2)解:∵CE,BE是⊙O的切线,
∴CE=BE,
∵OE⊥BC,OD=DE,
∴OC=CE,OB=BE,
∴OC=OB=BE=CE,
∴四边形OBEC是菱形,
∵∠OBE=90°,
∴四边形OBEC是正方形,
∴∠BOC=90°,
∴∠AOC=90°,
∵AB=6,
∴AO=OC=OB=3,
∴由![]() ,线段BC,AB所围成图形的面积=S扇形AOC+S△BCO=
,线段BC,AB所围成图形的面积=S扇形AOC+S△BCO=![]() +
+![]() ×3×3=
×3×3=![]() π+
π+![]() .
.

【题目】为贯彻落实省教育厅提出的“三生教育”.在母亲节来临之际,某校团委组织了以“珍爱生命,
学会生存,感恩父母”为主题的教育活动,在学校随机调查了50名同学平均每周在家做家务的时间,统
计并制作了如下的频数分布表和扇形统计图:
组别 | 做家务的时间 | 频数 | 频率 |
A | 1≤t<2 | 3 | 0.06 |
B | 2≤t<4 | 20 | 0.40 |
C | 4≤t<6 | a | 0.30 |
D | 6≤t<8 | 8 | b |
E | t≥8 | 4 | 0.08 |
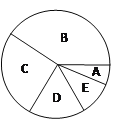
根据上述信息回答下列问题:
(1)a= ,b= .
(2)在扇形统计图中,B组所占圆心角的度数为 .
(3)全校共有2000名学生,估计该校平均每周做家务时间不少于4小时的学生约有多少人?