题目内容
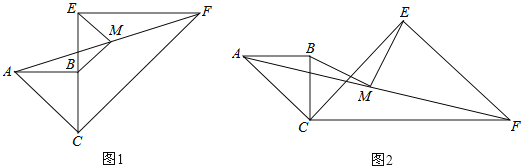
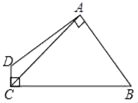
【题目】(几何背景)如图1,AD为锐角△ABC的高,垂足为D.求证:AB2﹣AC2=BD2﹣CD2
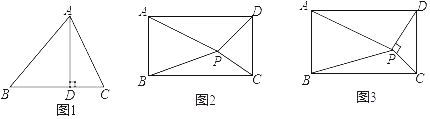
(知识迁移)如图2,矩形ABCD内任意一点P,连接PA、PB、PC、PD,请写出PA、PB、PC、PD之间的数量关系,并说明理由.
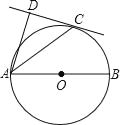
(拓展应用)如图3,矩形ABCD内一点P,PC⊥PD,若PA=a,PB=b,AB=c,且a、b、c满足a2﹣b2=![]() c2,则
c2,则![]() 的值为 (请直接写出结果)
的值为 (请直接写出结果)
【答案】【几何背景】:详见解析;【知识迁移】:详见解析;【拓展应用】:![]()
【解析】
几何背景:由 Rt△ABD中,AD2=AB2﹣BD2,Rt△ACD中,AD2=AC2﹣CD2,则结论可证.
知识迁移:过P点作PE⊥AD,延长EP交BC于F,可证四边形ABFE,四边形DCFE是矩形.根据上面的结论求得PA、PB、PC、PD之间的数量关系.
拓展应用:根据勾股定理可列方程组,可求PD=![]() c,PC=
c,PC=![]() c即可得
c即可得![]() .
.
解:几何背景:在Rt△ABD中,AD2=AB2﹣BD2
Rt△ACD中,AD2=AC2﹣CD2,
∴AB2﹣BD2=AC2﹣CD2,
∴AB2﹣AC2=BD2﹣CD2.
知识迁移:BP2﹣PC2 =BF2﹣CF2.
如 图:
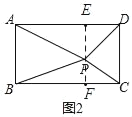
过P点作PE⊥AD,延长EP交BC于F
∴四边形ABCD是矩形
∴AD∥BC∠BAD=∠ADC=∠DCB=∠ABC=90°
又∵PE⊥AD
∴PF⊥BC
∵PE是△APD的高
∴PA2﹣PD2=AE2﹣DE2.
∵PF是△PBC的高
∴BP2﹣PC2 =BF2﹣CF2.
∵∠BAD=∠ADC=∠DCB=∠ABC=90°,PE⊥AD,PF⊥BC
∴四边形ABFE,四边形DCFE是矩形
∴AE=BF,CF=DE
∴PA2﹣PD2=BP2﹣PC2.
拓展应用:∵PA2﹣PD2=BP2﹣PC2.
∴PA2﹣PB2=![]() c2.
c2.
∴PD2﹣PC2=![]() c2.
c2.
且PD2+PC2=c2.
∴PD=![]() c,PC=
c,PC=![]() c
c
∴![]() ,
,
故答案为![]() .
.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案