题目内容
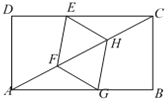
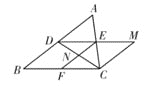
【题目】如图， 在三边互不相等的△ABC中， D，E，F分别是AB，AC，BC边的中点．连接DE，过点C作CM∥AB交DE的延长线于点M，连接CD、EF交于点N，则图中全等三角形共有（ ）
A.3对B.4对C.5对D.6对
【答案】C
【解析】
利用已知条件可证得DE，EF都是△ABC的中位线，同时可证得AE=EC，CF=
BC，利用三角形中位线定理可得到DE=BC，DE∥BC，EF∥AB，从而可以推出∠EDC=∠FCN，DE=CF，再利用AAS证明△DEN≌△CFN，然后利用有两组对边平行的四边形是平行四边形，可证得四边形EFCM是平行四边形，再利用平行四边形的性质可以推出△EMC≌△CFE，△ADE≌△CME，△ADE≌△CEF, △BCD≌△MDC．
证明：∵D，E，F分别是AB，AC，BC边的中点．
∴CF=BC，DE是△ABC的中位线，EF是△ABC的中位线，AE=EC
∴DE=BC，DE∥BC，EF∥AB，
∴∠EDC=∠FCN，DE=CF
在△DEN和△CFN中
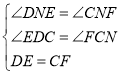
∴△DEN≌△CFN（AAS）；
∵EF∥AB，CM∥AB
∴EF∥CM，DE∥BC
∴四边形EFCM是平行四边形，
∴EM=CF=DE，EF=CM,
在△EMC和△CFE中，
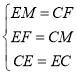
∴△EMC≌△CFE（SSS）；
在△ADE和△CME中，
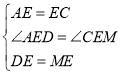
∴△ADE≌△CME（SAS）；
∴△ADE≌△CEF，
∴DE∥BC
又BD∥CM∥EF
∴四边形DBCM是平行四边形，
∴△BCD≌△MDC
∴图中的全等三角形一共有5对．
故答案为：C．
练习册系列答案
作业辅导系列答案
相关题目
