题目内容
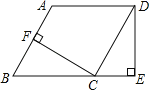
【题目】在矩形ABCD中，AB＝4，AD＝10，E是AD的一点，且AE＝2，M是AB上一点，射线ME交CD的延长线于点F，EG⊥ME交BC于点G，连接MG，FG，FG交AD于点N．
（1）当点M为AB中点时，则DF＝ ，FG＝ ．（直接写出答案）
（2）在整个运动过程中，
的值是否会变化，若不变，求出它的值；若变化，请说明理由．
（3）若△EGN为等腰三角形时，请求出所有满足条件的AM的长度．
【答案】（1）8，
；（2）在整个运动过程中，
的值不会变化，理由详见解析；（3）当AM＝﹣1+
或1或
时，△EGN为等腰三角形．
【解析】
（1）如图1，过G作GH⊥AD于H，先证明AE＝AM＝2，得∠AEM＝∠DEF＝45°，则DF＝DE＝8，再求CG的长，根据勾股定理计算FG的长；
（2）根据ME⊥EG，证明△AME∽△HEG，△EHG∽△FDE，可得tan∠EGM＝
＝tan∠EFG＝
，可得∠EGM＝∠EFG．可得∠MGF＝90°，由三角函数定义可得结论；
（3）设AM＝m，则BM＝4﹣m，DF＝4m，证明△MBG∽△GCF，表示CG＝8﹣2m，BG＝2+2m．分三种情况进行讨论，根据平行线分线段成比例定理和三角函数定义列等式可得结论．
（1）如图1，过G作GH⊥AD于H，
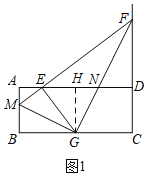
∵点M为AB中点，AB＝4，
∴AM＝2，
∵AE＝2，
∴AE＝AM＝2，
∴DE＝10﹣2＝8，
∵四边形ABCD是矩形，
∴∠A＝∠CDA＝90°，
∴∠AEM＝∠DEF＝45°，
∴DF＝DE＝8，
∵EG⊥ME，
∴∠MEG＝90°，
∴∠HEG＝∠EGH＝45°，
∴GH＝EH＝4，
∴CG＝DH＝10﹣2﹣4＝4，
Rt△FGC中，FG2＝CG2+CF2，
FG＝
；
（2）在整个运动过程中，的值不会变化，理由是：
如图1，过点G作GH⊥AD于点H，
∵ME⊥EG，
∴△AME∽△HEG，△EHG∽△FDE，
∴
，
，
∴
，
，
∴∠EGM＝∠EFG．
∵∠EGF+∠EFG＝90°，
∴∠EGF+∠EGM＝90°，即∠MGF＝90°，
∴
．
（3）设AM＝m，则BM＝4﹣m，DF＝4m，
∴CF＝4+4m．
由（2）得∠MGF＝90°，
∴△MBG∽△GCF，
∴
，
∴
，
∴CG＝8﹣2m，BG＝2+2m．
分三种情况：
ⅰ）当EG＝NG时，如图2，过点G作GH⊥AD于点H，则EH＝HN＝2m，
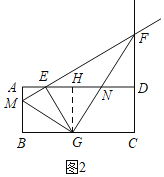
∴DN＝（8﹣2m）﹣2m＝8﹣4m．
∵DN∥CG，
∴
，即
，
∴m＝﹣1±，
解得m＝﹣1+或m＝﹣1﹣（舍去）．
∴AM＝﹣1；
ⅱ） 当EN＝NG时，∠NEG＝∠NGE．
∵AD∥BC，
∴∠NEG＝∠EGB，
∴∠EGB＝∠NGE．
如图3，过点E作EK⊥BC于点K，则KG＝8﹣（8﹣2m）＝2m，
∴
，
∴
，
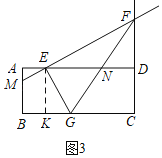
∴m＝1．
ⅲ）当EN＝EG时，如图4，∠ENG＝∠EGN．
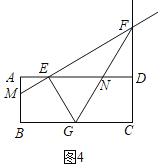
∵AD∥BC，
∴∠ENG＝∠DGC，
∴∠EGN＝∠DGC．
∴
，
∴
∴
．
综上所述：当AM＝﹣1+或1或时，△EGN为等腰三角形．
