��Ŀ����
����Ŀ����������С��ͬ�ĵ���ֱ�����ǰ尴��һ���Ĺ�����ã�����ͬһƽ���ڽ�ֱ�Ƕ�����ϡ�.
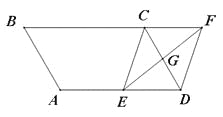
��1��ͼ1��һ�ַ���λ�ü�����������ļ���ͼ�Σ�![]() ��
��![]() ��
��![]() ��ͬһ��ֱ���ϣ�����
��ͬһ��ֱ���ϣ�����![]() . ���ҳ�ͼ�е�ȫ�������Σ������в���δ��ʶ����ĸ������˵�����ɣ�
. ���ҳ�ͼ�е�ȫ�������Σ������в���δ��ʶ����ĸ������˵�����ɣ�
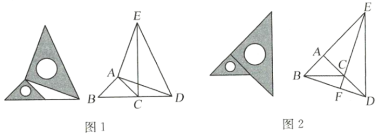
��2��ͼ2Ҳ��һ�ַ���λ�ü�����������ļ���ͼ�Σ�![]() ��
��![]() ��
��![]() ��ͬһ��ֱ���ϣ�����
��ͬһ��ֱ���ϣ�����![]() ��
��![]() �����ӳ�
�����ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() .���ҳ��߶�
.���ҳ��߶�![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
��3�����㣺
�ٻ���һ�����Ϸ��ù����Ҳ�ͬ��ͼ1��ͼ2����λ�õļ���ͼ�Σ�
��д������������ͼ�����߶�![]() ��
��![]() ��λ�ú�������ϵ��
��λ�ú�������ϵ��
������ڢ����еĽ����ڰ��չ��������������ļ���ͼ���ж�������
���𰸡���1��![]() ��֤�������������2��
��֤�������������2��![]() ��֤�������������3���������������
��֤�������������3���������������![]() ��
��![]() ���۴���
���۴���
��������
��1����֤��BAD����CAE������SAS֤����ABD���ACEȫ�ȣ�
��2������SAS֤����ABD���ACEȫ�ȣ���BD��CE����ADB����AEC�������������ڽǺͶ���֤����CFD����CAE��90����ж�λ�ù�ϵ��
��3������ABC�Ƶ�A��ת���ADE�ص�ʱ�����Գ�����
��1��![]()
![]() �ǵ���ֱ��������
�ǵ���ֱ��������
![]() ��
��![]()
ͬ��![]() ��
��![]()
![]()
![]()
��![]()
��![]() ��
��![]() ��
��
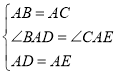
![]()
��2��![]()
֤�����£���![]() ��
��![]() ��
��
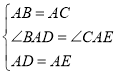
![]()
![]()
![]()
![]()
![]()
![]()
![]()
��![]()
![]()
��3������ͼ������ABC�Ƶ�A��ת���ADE�ص�ʱ
��![]() ��
��![]()
�����ڣ�֤�����£�
��![]()
��![]()
��![]() ��
��![]() ��
��
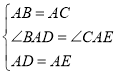
![]()
��![]()
![]()
��![]()
��![]() ������ADE=45����
������ADE=45����
��![]() =90����
=90����
![]()
��![]() ��
��![]() ����.
����.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ijУ�ٰ���һ��Ȥζ��ѧ����������100�֣�ѧ���÷־�Ϊ�������ﵽ�ɼ�60�ּ�����Ϊ�ϸﵽ90�ּ�����Ϊ���㣬��ξ����У���������ѧ���ɼ����£����飺30,60,60��60,60,60,70,90,90,100 �����飺50,60,60,60,70,70,70,70,80,90.
��1�����ϳɼ�ͳ�Ʒ�������a=______�֣�b=______�֣�c=_______�֣�
��� | ƽ���� | ��λ�� | ���� | �ϸ��� | ������ |
���� | 68�� | a | 376 | 30% | |
���� | b | c | 90% |
��2��С��ͬѧ˵����ξ����ҵ���70�֣�������С��������������ƫ�ϣ��۲���������жϣ�С�������Ǽ����ĸ����ѧ������˵������
��3����������ķ���������ʣ�������Ǹ�У��ѧ�����Ľ���Ա��������Ҫ��ѡһ��ͬѧ����ѧУ�μӸ��������ѡ����һ�飿��˵������