题目内容
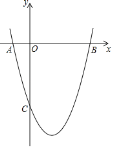
【题目】如图,长度为5的动线段AB分别与坐标系横轴、纵轴的正半轴交于点A、点B,点O和点C关于AB对称,连接CA、CB,过点C作x轴的垂线段CD,交x轴于点D
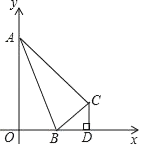
(1)移动点A,发现在某一时刻,△AOB和以点B、D、C为顶点的三角形相似,求这一时刻点C的坐标;
(2)移动点A,当![]() 时求点C的坐标.
时求点C的坐标.
【答案】(1)点![]() 的坐标为
的坐标为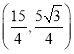 ;(2)
;(2)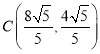 .
.
【解析】
(1)根据轴对称的性质得:AB是OC的垂直平分线,由垂直平分线的性质得:OB=BC,OA=AC,△AOB和以点B、D、C为顶点的三角形相似,存在两种情况:
①当∠ABO=∠CBD时,②当∠ABO=∠BCD时,根据角的关系分别计算点C的坐标即可;
(2)先根据三角函数定义求OB=![]() ,OA=2
,OA=2![]() ,利用面积法得OG和OC的长,根据等角的三角函数可知:OG=2BG,证明△BGO∽△CDO,列比例式可得结论.
,利用面积法得OG和OC的长,根据等角的三角函数可知:OG=2BG,证明△BGO∽△CDO,列比例式可得结论.
(1)连接![]() ,交
,交![]() 于
于![]() ,
,
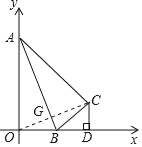
∵点![]() 和点
和点![]() 关于
关于![]() 对称,
对称,
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 和以点
和以点![]() 为顶点的三角形相似,存在两种情况:
为顶点的三角形相似,存在两种情况:
①当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
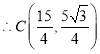 ;
;
②当![]() 时,
时,![]() ,
,
![]() ,
,
![]() 轴,
轴,
![]() 轴,此种情况不成立;
轴,此种情况不成立;
综上所述,![]() 和以点
和以点![]() 为顶点的三角形相似,这一时刻点
为顶点的三角形相似,这一时刻点![]() 的坐标为
的坐标为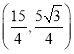 ;
;
(2)![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() 或
或![]() (舍),
(舍),
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
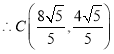 .
.

练习册系列答案
相关题目