题目内容
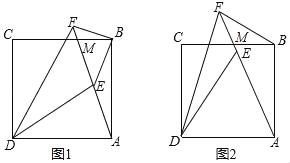
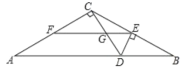
【题目】如图,已知EF是△ABC的中位线,DE⊥BC交AB于点D,CD与EF交于点G,若CD⊥AC,EF=8,EG=3,则AC的长为___________.
【答案】8
【解析】
由三角形中位线定理得出AB=2EF=16,EF∥AB,AF=CF,CE=BE,证出GE是△BCD的中位线,得出BD=2EG=6,AD=AB-BD=10,由线段垂直平分线的性质得出CD=BD=6,再由勾股定理即可求出AC的长.
∵EF是△ABC的中位线,
∴AB=2EF=16,EF∥AB,AF=CF,CE=BE,
∴G是CD的中点,
∴GE是△BCD的中位线,
∴BD=2EG=6,
∴AD=AB-BD=10,
∵DE⊥BC,CE=BE,
∴CD=BD=6,
∵CD⊥AC,
∴∠ACD=90°,
∴AC=![]() ;
;
故答案为:8.

练习册系列答案
相关题目