题目内容
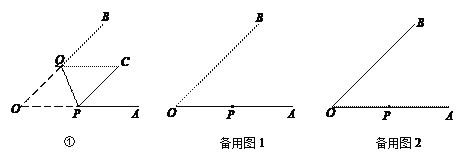
【题目】图①是一张∠AOB=45°的纸片折叠后的图形,P、Q分别是边OA、OB上的点,且OP=2 cm.将∠AOB沿PQ折叠,点O落在纸片所在平面内的C处.
(1)①当PC∥QB时,OQ= cm;
②在OB上找一点Q,使PC⊥QB(尺规作图,保留作图痕迹);
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.
【答案】(1)2;见解析(2)当点C在∠AOB的内部或一边上时,则重叠部分即为△CPQ
【解析】分析:(1)①证明四边形,即可得OQ=OP=2cm;②分点C、P在BQ同侧和异侧两种情况作图即可;(3)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;点C在∠AOB的内部或一边上时,由折叠的性质、三角形内角和定理以及解直角三角形即可求出OQ的长;点C在∠AOB的外部时,同理求出OQ的长即可.
详解:
(1)①当PC∥QB时,∠O=∠CPA,
由折叠的性质得:∠C=∠O,OP=CP,
∴∠CPA=∠C,
∴OP∥QC,
∴四边形OPCQ是平行四边形,
∴四边形OPCQ是菱形,
∴OQ=OP=2cm;
故答案为:2cm;
② 分点C、P在BQ同侧和异侧两种情况,画对一种就给全分;
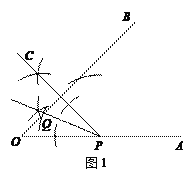
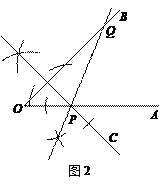
(2)当点C在∠AOB的内部或一边上时,则重叠部分即为△CPQ.
因为△CPQ是由△OPQ折叠得到,所以当△OPQ为等腰三角形时,重叠部分必为等腰三角形.
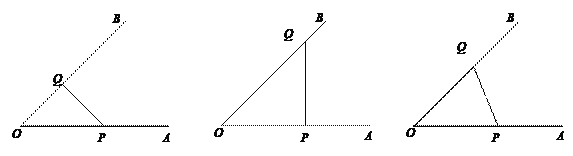 如图1、2、3三种情况:
如图1、2、3三种情况:
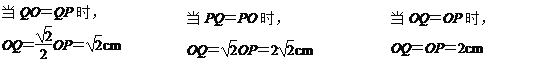

当点C在∠AOB的外部时,
当点C在射线OB的上方时(如图4), 当点C在射线OA的下方时(如图5),
OQ=![]() -
-![]() (cm)
(cm)
OQ=![]() +
+![]() (cm)
(cm)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某天,一蔬菜经营户用180元钱从蔬菜批发市场批了西红柿和豆角共40千克到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/千克) | 3.6 | 4.6 |
零售价(单位:元/千克) | 5.4 | 7.5 |
问:他当天卖完这些西红柿和豆角能赚多少钱?