题目内容
【题目】如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O-D-E-F表示y1与x的函数图像;折线O-G-F表示y2与x的函数图像.

(1)小明的速度为_________m/min,图②中a的值为__________.
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.
①写出小明妈妈在骑车由C处返回到A处的过程中,y与x的函数表达式及x的取值范围;

②在图③中画出整个过程中y与x的函数图像.(要求标出关键点的坐标)

【答案】 60 33
【解析】试题分析:
(1)由图可知,①C处距离学校1800米,小明从C处到学校用时30分钟,由此即可求得小明的速度为1800÷30=60(米/分钟);②C处距离小明家2400米,小明妈妈从C处到家再到C处用时24分钟,由此可得小明妈妈的速度为2400×2÷24=200(米/分钟),由此可得a=(2400×2+1800)÷200=33(分钟);
(2)①由(1)可知小明妈妈的速度为200米/分钟,小明的速度为60米/分钟可得y=260x(![]() );②由题意可知,y与x的函数关系分为三段:第一段
);②由题意可知,y与x的函数关系分为三段:第一段![]() ,第二段
,第二段![]() ,第三段
,第三段![]() ,结合题中已知条件可得当
,结合题中已知条件可得当![]() 时,y=0;当x=12时,y=3120;当x=30时,y=600;当x=33时,y=0;由此即可画出整个过程中y与x的函数图象了.
时,y=0;当x=12时,y=3120;当x=30时,y=600;当x=33时,y=0;由此即可画出整个过程中y与x的函数图象了.
试题解析:
(1)①由图1和图2中的信息可知:C处距离学校1800米,小明由C处到学校用了30分钟,
∴小明的速度=1800÷30=60(米/分钟);
②由图1和图2中的信息可知: C处距离小明家2400米,小明妈妈从C处到家再到C处用时24分钟,
∴小明妈妈的速度为2400×2÷24=200(米/分钟),
∵C处距离学校1800米,
∴a=(2400×2+1800)÷200=33(分钟);
(2)①由(1)可知小明妈妈的速度是:200 米/分钟,小明的速度是60米/分钟,
∵小明妈妈在骑车由C回到A的过程中,小明与妈妈背向而行,
∴y=260x, x的取值范围是0≤x≤12.
②由题意可得,整个过程中,y与x的函数图象如下图所示:
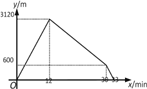 .
.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】某天,一蔬菜经营户用180元钱从蔬菜批发市场批了西红柿和豆角共40千克到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/千克) | 3.6 | 4.6 |
零售价(单位:元/千克) | 5.4 | 7.5 |
问:他当天卖完这些西红柿和豆角能赚多少钱?
【题目】某企业为打入国际市场,决定从![]() 、
、![]() 两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)
两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)
项目 类别 | 年固定 成本 | 每件产品 成本 | 每件产品 销售价 | 每年最多可 生产的件数 |
|
|
|
|
|
|
|
|
|
|
其中年固定成本与年生产的件数无关,![]() 为待定常数,其值由生产
为待定常数,其值由生产![]() 产品的原材料价格决定,预计
产品的原材料价格决定,预计![]() .另外,年销售
.另外,年销售![]() 件
件![]() 产品时需上交
产品时需上交![]() 万美元的特别关税.假设生产出来的产品都能在当年销售出去.
万美元的特别关税.假设生产出来的产品都能在当年销售出去.
![]() 写出该厂分别投资生产
写出该厂分别投资生产![]() 、
、![]() 两种产品的年利润
两种产品的年利润![]() ,
,![]() 与生产相应产品的件数
与生产相应产品的件数![]() 之间的函数关系并指明其自变量取值范围;
之间的函数关系并指明其自变量取值范围;
![]() 如何投资才可获得最大年利润?请你做出规划.
如何投资才可获得最大年利润?请你做出规划.










