ΧβΡΩΡΎ»ί
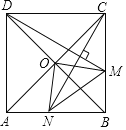
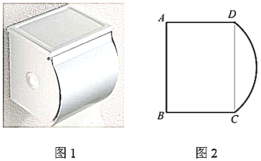
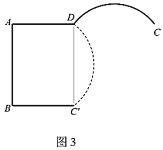
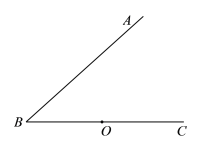
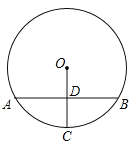
ΓΨΧβΡΩΓΩΈ“ΙζΙ≈¥ζ ΐ―ßΦ“’‘Υ§άϊ”Οœ“ΆΦ÷ΛΟςΝΥΙ¥Ι…Ε®άμΘ§’β «÷χΟϊΒΡ’‘Υ§œ“ΆΦΘ®»γΆΦ1Θ©Θ°Υϋ «”…ΥΡΗω»ΪΒ»ΒΡ÷±Ϋ«»ΐΫ«–ΈΤ¥≥…ΝΥΡΎΓΔΆβΕΦ «’ΐΖΫ–ΈΒΡΟάάωΆΦΑΗΘ°‘Ύœ“ΆΦ÷–Θ®»γΆΦ2Θ©Θ§“―÷ΣΒψOΈΣ’ΐΖΫ–ΈABCDΒΡΕ‘Ϋ«œΏBDΒΡ÷–ΒψΘ§Ε‘Ϋ«œΏBDΖ÷±πΫΜAHΘ§CF”ΎΒψPΓΔQΘ°‘Ύ’ΐΖΫ–ΈEFGHΒΡEHΓΔFGΝΫ±Ώ…œΖ÷±π»ΓΒψMΘ§NΘ§«“MNΨ≠ΙΐΒψOΘ§»τMHΘΫ3MEΘ§BDΘΫ2MNΘΫ4![]() Θ°‘ρΓςAPDΒΡΟφΜΐΈΣ_____Θ°
Θ°‘ρΓςAPDΒΡΟφΜΐΈΣ_____Θ°
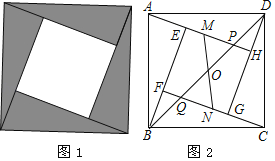
ΓΨ¥πΑΗΓΩ5
ΓΨΫβΈωΓΩ
Ν§Ϋ”FHΘ§ΉςEKΓΈMNΘ§OLΓΆDGΘ§Ά®Ιΐ’ΐΖΫ–ΈΒΡ–‘÷ ΚΆ»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ “‘ΦΑΙ¥Ι…Ε®άμΩ…«σEMΘΫ1Θ§Ω…ΒΟEHΘΫ4Θ§”…Ι¥Ι…Ε®άμΩ…«σHDΘΫ2Θ§AHΘΫ6Θ§”…ΤΫ––œΏΒΡ–‘÷ Ω…ΒΟPHΘΫ1Θ§Φ¥Ω…«σΫβΘ°
»γΆΦΘ§Ν§Ϋ”FHΘ§ΉςEKΓΈMNΘ§OLΓΆDG
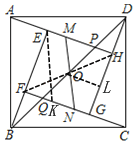
ΓΏΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§«“BDΘΫ2MNΘΫ4![]()
ΓύMNΘΫ2![]() Θ§ABΘΫ2
Θ§ABΘΫ2![]()
ΓΏΥΡ±Ώ–ΈEFGH «’ΐΖΫ–Έ
ΓύFOΘΫHOΘ§EHΓΈFG
ΓύΓœHMOΘΫΓœFNOΘ§ΓœMHOΘΫΓœNFOΘ§«“FOΘΫHO
ΓύΓςMHOΓ’ΓςFNOΘ®AASΘ©
ΓύMHΘΫFN
ΓΏMHΘΫ3MEΘ§
ΓύMHΘΫFNΘΫ3EMΘ§EHΘΫEFΘΫ4EM
ΓύEKΓΈKNΘ§EHΓΈFG
ΓύΥΡ±Ώ–ΈEMNK «ΤΫ––ΥΡ±Ώ–Έ
ΓύMNΘΫEKΘΫ2![]() Θ§KNΘΫEM
Θ§KNΘΫEM
ΓύFKΘΫ2EM
ΓΏEF2+FK2ΘΫEK2Θ§
Γύ16EM2+4EM2ΘΫ20
ΓύEMΘΫ1
ΓύEHΘΫ4Θ§
ΓΏAD2ΘΫΘ®AE+4Θ©2+DH2Θ§«“AEΘΫDH
ΓύDHΘΫAEΘΫ2
ΓύAHΘΫ6
ΓΏPHΓΈOL
Γύ![]()
ΓύPHΘΫ1
ΓύAPΘΫ5
ΓύSΓςAPDΘΫ![]() ΓΝ5ΓΝ2ΘΫ5
ΓΝ5ΓΝ2ΘΫ5
Ι ¥πΑΗΈΣΘΚ5.

 –Γ―ßΕαΙΎABΨμœΒΝ–¥πΑΗ
–Γ―ßΕαΙΎABΨμœΒΝ–¥πΑΗ