Question

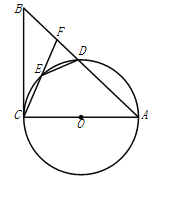
【题目】如图，在⊙O中，弦AB垂直平分半径OC，垂足为D．若点P是⊙O上异于点A，B的任意一点，则∠APB=（ ）

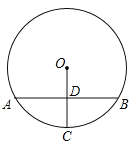
A.30°或60°B.60°或150°C.30°或150°D.60°或120°

Answer 1

【答案】D

【解析】

利用垂径定理及已知可得到∠OAD=30°，再求出∠AOB的度数，再分情况讨论：当点P在优弧AB上时，利用圆周角定理就可取出∠P的度数；当点P在劣弧上时，利用圆内接四边形的对角互补，就可求出∠AP1B的度数．

连接OA，OB，

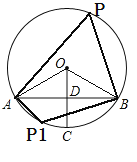
∵ 弦AB垂直平分半径OC

∴OD=OA，

∴∠OAD=30°，

∵OA=OB

∴∠OAB=∠OBA=30°，

∴∠AOB=180°-∠OAB-∠OBA=180°-30°-30°=120°；

当点P在优弧AB上时

∠APB=∠AOB=×120°=60°；

当点P在劣弧上时，

∠APB+∠AP1B=180°

∴∠AP1B=180°-60°=120°．

∴∠APB=120°或60°．

故答案为：D．