��Ŀ����
����Ŀ����ͼ��ֱ��y=kx+b��k��0����������y=ax2��a��0������A��B���㣬�ҵ�A�ĺ�������-2����B�ĺ�������3�������½��ۣ�
��������y=ax2��a��0����ͼ��Ķ���һ����ԭ�㣻
��x��0ʱ��ֱ��y=kx+b��k��0����������y=ax2��a��0���ĺ���ֵ������x�����������
��AB�ij��ȿ��Ե���5��
�ܡ�OAB�п��ܳ�Ϊ�ȱ������Σ�
����-3��x��2ʱ��ax2+kx��b��
������ȷ�Ľ����ǣ� ��

A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �ۢܢ�
���𰸡�B
��������������������ɶ������깫ʽ�жϼ��ɣ�
������ͼ��õ�һ�κ���y=kx+bΪ�������������ߵ�x����0ʱΪ����������ѡ����ȷ��
��AB��������Ϊ5����A��B�ĺ��������ABΪ5ʱ��ֱ��AB��x��ƽ�У���k=0������֪ì�ܣ�
��������OAB������Ϊ�ȱ������Σ���ΪOA��OB��������ȣ�
��ֱ��y=-kx+b��y=kx+b����y��Գƣ������Գƺ��ͼ��y=-kx+b�������߽��������ֱ�Ϊ-3��2���ҳ�һ�κ���ͼ�����������Ϸ�ʱx�ķ�Χ�жϼ��ɣ�
�����������������y=ax2�����ö������깫ʽ�ã���������Ϊ��0��0������ѡ����ȷ��
������ͼ��ã�ֱ��y=kx+b��k��0��Ϊ��������������y=ax2��a��0����x��0ʱΪ����������x��0ʱ��ֱ���������ߺ���ֵ������x�����������ѡ����ȷ��
����A��B������ֱ�Ϊ-2��3����AB=5���ɵó�ֱ��AB��x��ƽ�У���k=0������֪k��0ì�ܣ���AB������Ϊ5����ѡ�����
����OA=OB���õ�ֱ��AB��x��ƽ�У���k=0������֪k��0ì�ܣ���OA��OB������AOB������Ϊ�ȱ������Σ���ѡ�����
��ֱ��y=-kx+b��y=kx+b����y��Գƣ���ͼ��ʾ��
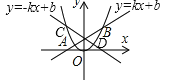
�ɵó�ֱ��y=-kx+b�������߽���C��D������ֱ�Ϊ-3��2����ͼ��ɵã���-3��x��2ʱ��ax2��-kx+b����ax2+kx��b��
����ȷ�Ľ������٢ڢ���
��ѡB��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�