题目内容
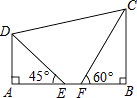
【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.

【答案】(1)证明见解析;
(2)四边形CENF是平行四边形,理由见解析.
【解析】(1)证明:∵四边形ABCD是正方形,
∴DC=DA,∠DCE=∠DAM=90°,
在△DCE和△MDA中,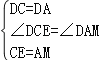 ,
,
∴△DCE≌△MDA(SAS),
∴DE=DM,∠EDC=∠MDA.
又∵∠ADE+∠EDC=∠ADC=90°,
∴∠ADE+∠MDA=90°,
∴DE⊥DM;
(2)解:四边形CENF是平行四边形,理由如下:
∵四边形ABCD是正方形,
∴AB∥CD,AB=CD.
∵BF=AM,
∴MF=AF+AM=AF+BF=AB,
即MF=CD,
又∵F在AB上,点M在BA的延长线上,
∴MF∥CD,
∴四边形CFMD是平行四边形,
∴DM=CF,DM∥CF,
∵NM⊥DM,NE⊥DE,DE⊥DM,
∴四边形DENM都是矩形,
∴EN=DM,EN∥DM,
∴CF=EN,CF∥EN,
∴四边形CENF为平行四边形.

练习册系列答案
相关题目