题目内容
抛物线y=(k2-2)x2-4kx+m的对称轴是直线x=2,且它的最低点在直线y=-2x+2上,求:
(1)函数解析式;
(2)若抛物线与x轴交点为A、B与y轴交点为C,求△ABC面积.
(1)函数解析式;
(2)若抛物线与x轴交点为A、B与y轴交点为C,求△ABC面积.
(1)∵抛物线y=(k2-2)x2-4kx+m的对称轴是直线x=2
∴
=2
解得k=-1或k=2
又∵图象有最低点,即开口向上
∴k2-2>0,即k2>2
∴k=2
即y=2x2-8x+m
把x=2代入直线y=-2x+2得
y=-2
即抛物线的顶点坐标是(2,-2)
代入函数y=2x2-8x+m得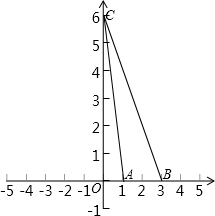
m=6
∴函数解析式为y=2x2-8x+6;
(2)当x=0时,y=6,即点C的坐标是(0,6)
当y=0时,2x2-8x+6=0,解得x=1或x=3,
即点A、B的坐标分别是(1,0)、(3,0)
则AB=3-1=2,OC=6
∴S△ABC=
AB•OC=
×2×6=6.
∴
| 4k |
| 2(k2-2) |
解得k=-1或k=2
又∵图象有最低点,即开口向上
∴k2-2>0,即k2>2
∴k=2
即y=2x2-8x+m
把x=2代入直线y=-2x+2得
y=-2
即抛物线的顶点坐标是(2,-2)
代入函数y=2x2-8x+m得

m=6
∴函数解析式为y=2x2-8x+6;
(2)当x=0时,y=6,即点C的坐标是(0,6)
当y=0时,2x2-8x+6=0,解得x=1或x=3,
即点A、B的坐标分别是(1,0)、(3,0)
则AB=3-1=2,OC=6
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目

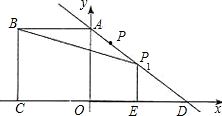 形BCEP1的面积为S,请问S是否有最大值?若有,请求出P点坐标和S的最大值;若没有,请说明理由.
形BCEP1的面积为S,请问S是否有最大值?若有,请求出P点坐标和S的最大值;若没有,请说明理由.
 且与OE平行,现正方形以每秒
且与OE平行,现正方形以每秒
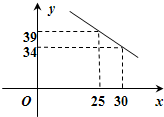 4万元,且所有资金全部用于生产这三种型号的汽车,三种型号的汽车生产成本和售价如下表:
4万元,且所有资金全部用于生产这三种型号的汽车,三种型号的汽车生产成本和售价如下表: