题目内容
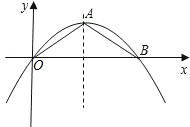
如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
(1)求抛物线的解析式;
(2)在抛物线上求点M,使△MOB的面积是△AOB面积的3倍;
(3)连接OA,AB,在x轴下方的抛物线上是否存在点N,使△OBN与△OAB相似?若存在,求出N点的坐标;若不存在,说明理由.
(1)求抛物线的解析式;
(2)在抛物线上求点M,使△MOB的面积是△AOB面积的3倍;
(3)连接OA,AB,在x轴下方的抛物线上是否存在点N,使△OBN与△OAB相似?若存在,求出N点的坐标;若不存在,说明理由.

(1)由题意,可设抛物线的解析式为y=a(x-2)2+1,
∵抛物线过原点,
∴a(0-2)2+1=0,a=-
.
∴抛物线的解析式为y=-
(x-2)2+1=-
x2+x.
(2)△AOB和所求△MOB同底不等高,且S△MOB=3S△AOB,
∴△MOB的高是△AOB高的3倍,即M点的纵坐标是-3.
∴-3=-
x2+x,即x2-4x-12=0.
解之,得x1=6,x2=-2.
∴满足条件的点有两个:M1(6,-3),M2(-2,-3)
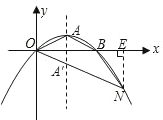
(3)不存在.
由抛物线的对称性,知AO=AB,∠AOB=∠ABO.
若△OBN与△OAB相似,必有∠BON=∠BOA=∠BNO,
即OB平分∠AON,
设ON交抛物线的对称轴于A'点,则A、A′关于x轴对称,
∴A'(2,-1).
∴直线ON的解析式为y=-
x.
由-
x=-
x2+x,得x1=0,x2=6.
∴N(6,-3).
过N作NE⊥x轴,垂足为E.在Rt△BEN中,BE=2,NE=3,
∴NB=
=
.
又∵OB=4,
∴NB≠OB,∠BON≠∠BNO,△OBN与△OAB不相似.
同理,在对称轴左边的抛物线上也不存在符合条件的N点.
所以在该抛物线上不存在点N,使△OBN与△OAB相似.
∵抛物线过原点,
∴a(0-2)2+1=0,a=-
| 1 |
| 4 |
∴抛物线的解析式为y=-
| 1 |
| 4 |
| 1 |
| 4 |
(2)△AOB和所求△MOB同底不等高,且S△MOB=3S△AOB,
∴△MOB的高是△AOB高的3倍,即M点的纵坐标是-3.
∴-3=-
| 1 |
| 4 |
解之,得x1=6,x2=-2.
∴满足条件的点有两个:M1(6,-3),M2(-2,-3)
(3)不存在.
由抛物线的对称性,知AO=AB,∠AOB=∠ABO.
若△OBN与△OAB相似,必有∠BON=∠BOA=∠BNO,
即OB平分∠AON,
设ON交抛物线的对称轴于A'点,则A、A′关于x轴对称,
∴A'(2,-1).
∴直线ON的解析式为y=-
| 1 |
| 2 |
由-
| 1 |
| 2 |
| 1 |
| 4 |
∴N(6,-3).
过N作NE⊥x轴,垂足为E.在Rt△BEN中,BE=2,NE=3,
∴NB=
| 22+32 |
| 13 |
又∵OB=4,
∴NB≠OB,∠BON≠∠BNO,△OBN与△OAB不相似.
同理,在对称轴左边的抛物线上也不存在符合条件的N点.
所以在该抛物线上不存在点N,使△OBN与△OAB相似.


练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目


 的长是方程x2-6x+5=0的两个实数根.
的长是方程x2-6x+5=0的两个实数根.