Question

【题目】在中，，，，点在所在的直线上运动，作（、、按逆时针方向）．

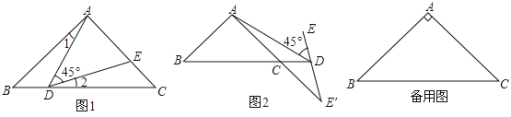
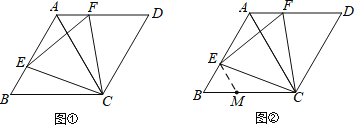
（1）如图①，当点在线段上运动时，交于．

①求证：．

②当是等腰三角形时，直接写出的长．

（2）如图②，当点在的延长线上运动，的反向延长线与的延长线相交于点，是否存在点，使是等腰三角形？若存在，写出点的位置；若不存在，请简要说明理由．

Answer 1

【答案】(1) ①证明见解析；②AE的值是1或 2或； (3)存在，D在BC的延长线上，且CD= 2

【解析】

(1) ①求出∠B=45°，根据三角形外角性质得出∠1+∠B=∠ADC=45°+∠2．求出即可；

②分为三种情况，①DE=AE,②AD=AE，③AD=DE，根据等腰三角形性质(等腰三角形两边相等)，三角形全等推出即可；

(2)存在，可证 得到CD=AC=2．

解(1) ①∵在Rt△ABC中，∠BAC=90°。AB=AC,

∴∠B=∠C=45°

∵∠ADE=45°,

∴∠ADC=∠B+∠1=∠ADE+∠2,

即45°+∠1=45°+∠2．

∴∠1=∠2．

②解:当△ADE是等腰三角形时，分为以下三种情况:

第一种情况: DE=AE,

∵DE=AE,

∴∠ADE=∠DAE=45°=∠C,

∴∠AED=90°，∠ADC=90° ,

即DE⊥．AC．

∴AD= DC．

∴E为AC的中点，

∴

第二种情况: AD=AE，此时D和B重合，E和C重合,

即AE=AC=2;

第三种情况: AD=DE,

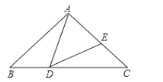
在△ABD和△DCE中．

∴ ,

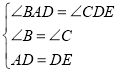
∴BD=CE，AB=DC,

设BD=CE=x,

在Rt△ABC中，∵∠BAC=90°, AB=AC=2,

∴BC= ．

∴DC=-x．

∴-x=2,

∴x=-2,

∴AE=

综合上述: AE的值是1或 2或

(3)解:存在，理由如下：

∵

∴

∵

∴

∴

又∵

∴

∴

又∵ ,

∴ ，

故存在点，使是等腰三角形，此时D在BC的延长线上，且CD= 2