题目内容
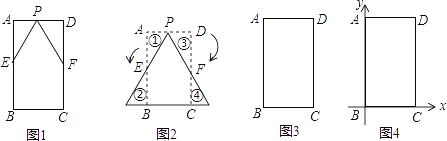
【题目】已知△ABC为等边三角形,P是直线AC上一点,AD⊥BP于D,以AD为边作等边△ADE(D,E在直线AC异侧).
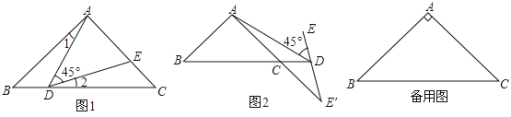
(1)如图1,若点P在边AC上,连CD,且∠BDC=150°,则![]() = ;(直接写结果)
= ;(直接写结果)
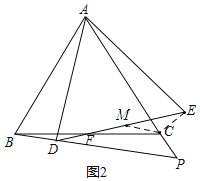
(2)如图2,若点P在AC延长线上,DE交BC于F求证:BF=CF;
(3)在图2中,若∠PBC=15°,AB=![]() ,请直接写出CP的长 .
,请直接写出CP的长 .
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】
(1)由题意可证△ABD≌△ACE,可得BD=CE,∠ABD=∠ACE,即可求∠EDC=60°,∠EDC=90°,则可得![]() 的值;
的值;
(2)过点CM∥BD交DE于点M,连接CE,由题意可证△ABD≌△ACE,可得BD=CE,∠AEC=∠ADB=90°,可求∠DEC=∠EMC=30°,可得MC=EC=BD,
则可证△BDF≌△CMF,可得BF=CF;
(3)作∠ABG=∠BAD,交AD于点G,由题意可求∠ABG=∠BAG=15°,可得∠BGD=30°,BG=AG,则可得BG=2BD,GD=![]() BD,AD=
BD,AD=![]() BD+2BD,根据勾股定理可求BD=1,AD=2+
BD+2BD,根据勾股定理可求BD=1,AD=2+![]() ,即可求AP的长,则可求CP的长.
,即可求AP的长,则可求CP的长.
(1)如图:连接CE
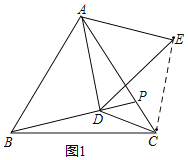
∵△ABC,△ADE是等边三角形,
∴AB=AC,AD=AE,∠DAE=∠BAC=60°,
∴∠BAD=∠CAE,且AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠ADB=90°,∠BDC=150°,∠ADE=60°,
∴∠EDC=60°,
∵∠BDC=∠BPC+∠ACD=∠BAC+∠ABD+∠ACD=60°+∠ACE+∠ACD=60°+∠ECD=150°
∴∠ECD=90°,
∴tan∠EDC=![]() ,
,
∴![]() ;
;
(2)如图:过点CM∥BD交DE于点M,连接CE
∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°=∠ADE=∠AED,
∴∠BAD=∠CAE,且AB=AC,AD=AE,
∴△ABD≌△ACE(ASA),
∴BD=CE,∠AEC=∠ADB=90°,
∵∠BDE=∠ADB+∠ADE,∠DEC=∠AEC-∠AED,
∴∠BDE=150°,∠DEC=30°,
∵MC∥BD,
∴∠DMC=∠BDE=150°,
∴∠EMC=30°,
∴∠DEC=∠EMC,
∴MC=CE,
∴BD=CM,且∠BDE=∠CMD,∠BFD=∠CFM,
∴△BDF≌△CMF(AAS),
∴CF=BF,
(3)如图:作∠ABG=∠BAD,交AD于点G
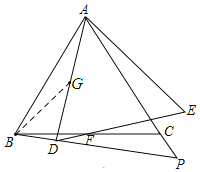
∵∠ABC=60°,∠PBC=15°,AD⊥BD,
∴∠DAB=15°,
∵∠ABG=∠BAD,
∴∠ABG=∠BAG=15°,
∴∠BGD=30°,BG=AG,
∴BG=2BD,GD=![]() BD,
BD,
∴AD=![]() BD+2BD,
BD+2BD,
在Rt△ABD中,AB2=BD2+AD2.
∴(![]() +
+![]() )2=(
)2=(![]() +2)2 BD2+BD2.
+2)2 BD2+BD2.
∴BD=1,
∴AD=2+![]() ,
,
∵∠BAD=15°,∠BAC=60°,
∴∠DAP=45°,且AD⊥BD,
∴AP=![]() AD=2
AD=2![]() +
+![]() ,
,
∵CP=AP-AC=AP-AB=2![]() +
+![]() -(
-(![]() +
+![]() ),
),
∴CP=![]() .
.
故答案为![]() .
.