题目内容
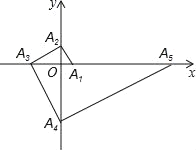
【题目】如图,已知△OAB的顶点A(6,0),B(0,2),O是坐标原点.将△OAB 绕点O按逆时针旋转90°得到△ODC.
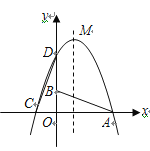
(1)写出C、D两点的坐标;
(2)求过C、D、A三点的抛物线的解析式,并求此抛物线的顶点M的坐标;
(3)在线段AB上是否存在点N使得MA=NM?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】C(-2,0),D(0,6);(2)![]() ,M(2,8);(3)存在,N(0,2).
,M(2,8);(3)存在,N(0,2).
【解析】
(1)根据旋转的性质,可得OC=OB,OD=OA,进而可得CD两点的坐标;
(2)设出解析式,并将A、C、D三点的坐标代入可得方程组,解可得解析式,进而可得M的坐标;
(3)假设存在并设出其坐标,连接MB,作ME⊥y轴于E,可得ME、BE、MB的长,进而可得BA与MB的关系,即可求出N的坐标,故可作出判断.
(1)C(2,0),D(0,6).
(2)设所求抛物线的解析式为![]()
∵A,C,D在抛物线上
∴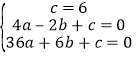 解得
解得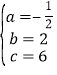 即
即 ![]()
又![]()
![]()
∴M(2,8).
(3) 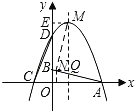
连接MB,作ME⊥y轴于E
则ME=2,BE=82=6
∴MB= ![]() ,BA=MB
,BA=MB
即在线段AB上存在点N(0,2)(即点B)使得NA=NM.

练习册系列答案
相关题目