题目内容
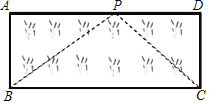
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.

【答案】(1)∠BOC=90°;(2)BE+CG =10cm;(3)OF=4.8cm.
【解析】试题分析:(1)连接OF,根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;再根据平行线性质得到∠BOC为直角;
(2)进而由切线长定理即可得到BE+CG的长;
(3)由勾股定理可求得BC的长,最后由三角形面积公式即可求得OF的长.
试题解析:(1)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°;
(2)∵OB=6cm,OC=8cm,
∴BC=10cm,
∴BE+CG=BC=10cm.
(3)OF=4.8


练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
【题目】“元旦”期间,某文具店购进 ![]() 只两种型号的文具进行销售,其进价和售价如表:
只两种型号的文具进行销售,其进价和售价如表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)该店用 ![]() 元可以购进A,B两种型号的文具各多少只?
元可以购进A,B两种型号的文具各多少只?
(2)在(![]() )的条件下,若把所购进A,B两种型号的文具全部销售完,利润率有没有超过
)的条件下,若把所购进A,B两种型号的文具全部销售完,利润率有没有超过 ![]() ?请你说明理由.
?请你说明理由.