Question

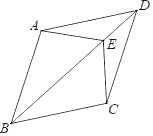
【题目】已知：如图，四边形ABCD中，AD∥BC，AD=CD，E是对角线BD上一点，且EA=EC．

（1）求证：四边形ABCD是菱形；

（2）如果∠BDC=30°，DE=2，EC=3，求CD的长．

Answer 1

【答案】（1）证明见解析；（2）CD的长为2．

【解析】

（1）首先证得△ADE≌△CDE，由全等三角形的性质可得∠ADE=∠CDE，由AD∥BC可得∠ADE=∠CBD，易得∠CDB=∠CBD，可得BC=CD，易得AD=BC，利用平行线的判定定理可得四边形ABCD为平行四边形，由AD=CD可得四边形ABCD是菱形；

（2）作EF⊥CD于F，在Rt△DEF中，根据30°的性质和勾股定理可求出EF和DF的长，在Rt△CEF中，根据勾股定理可求出CF的长，从而可求CD的长.

证明：（1）在△ADE与△CDE中，

，

∴△ADE≌△CDE（SSS），

∴∠ADE=∠CDE，

∵AD∥BC，

∴∠ADE=∠CBD，

∴∠CDE=∠CBD，

∴BC=CD，

∵AD=CD，

∴BC=AD，

∴四边形ABCD为平行四边形，

∵AD=CD，

∴四边形ABCD是菱形；

（2）作EF⊥CD于F.

∵∠BDC=30°，DE=2，

∴EF=1，DF=，

∵CE=3，

∴CF=2，

∴CD=2+．

.