题目内容
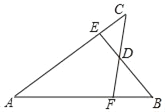
【题目】（1）如图，在△ABC中，∠ABC、∠ACB的平分线相交于F，过F作DE∥BC，分别交AB、AC于点D、E．判断DE=DB+EC是否成立？为什么？
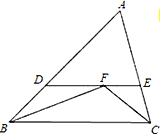
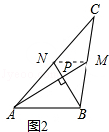
（2）如图，若点F是∠ABC的平分线和外角∠ACG的平分线的交点，其他条件不变，请猜想线段DE、DB、EC之间有何数量关系？
证明你的猜想。
【答案】（1）成立，证明见解析.（2）证明见解析.
【解析】试题分析： 
根据平行线的性质和角平分线的性质，得出
和
是等腰三角形，通过等量代换即可得出结论．
同
，只要求出
和
是等腰三角形即可．
试题解析：(1)成立；
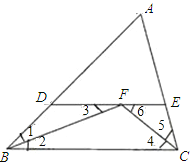
∵△ABC中BF、CF平分∠ABC、∠ACB，
∴∠1=∠2，∠5=∠4.
∵DE∥BC，∴∠2=∠3，∠4=∠6.
∴∠1=∠3，∠6=∠5.
根据在同一个三角形中，等角对等边的性质，可知：BD=DF，EF=CE.
∴DE=DF+EF=BD+CE.
故成立.
(2)∵BF分∠ABC，
∴∠DBF=∠FBC.
∴∠DFB=∠FBC.
∴∠ABF=∠DFB，
∴BD=DF.
∵CF平分∠ACG，
∴∠ACF=∠FCG.
∴∠DFC=∠FCG.
∴∠ACF=∠DFC，
∴CE=EF.
∴EF+DE=DF，即DE+EC=BD.
【题目】某县响应“建设环保节约型社会”的号召，决定资助部分村镇修建一批沼气池，使农民用到经济、环保的沼气能源．幸福村共有264户村民，政府补助村里34万元，不足部分由村民集资．修建A型、B型沼气池共20个．两种型号沼气池每个修建费用、可供使用户数、修建用地情况如下表：
沼气池 | 修建费用（万元/个） | 可供使用户数（户/个） | 占地面积（m2/个） |
A型 | 3 | 20 | 48 |
B型 | 2 | 3 | 6 |
政府相关部门批给该村沼气池修建用地708平方米．设修建A型沼气池x个，修建两种型号沼气池共需费用y万元．
（1）用含有x的代数式表示y；
（2）不超过政府批给修建沼气池用地面积，又要使该村每户村民用上沼气的修建方案有几种；
（3）若平均每户村民集资700元，能否满足所需费用最少的修建方案．
