题目内容
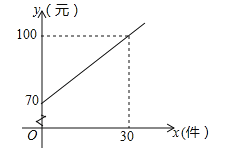
【题目】一只小球落在数轴上的某点
，第一次从向左跳1个单位到
，第二次从向右跳2个单位到
，第三次从向左跳3个单位到
，第四次从向右跳4个单位到
，若小球从原点出发，按以上规律跳了6次时，它落在数轴上的点
所表示的数是__________；若小球按以上规律跳了2n次时，它落在数轴上的点
所表示的数恰好是
，则这只小球的初始位置点所表示的数是__________.
【答案】3， 2．
【解析】
根据题意，可以发现题目中每次跳跃后相对于初始点的距离，从而可以解答本题．
解：由题意可得，
小球从原点出发，按以上规律跳了6次时，它落在数轴上的点P6所表示的数是6÷2=3，
小球按以上规律跳了2n次时，它落在数轴上的点P2n所表示的数恰好是n+2，则这只小球的初始位置点P0所表示的数是：n+2﹣（2n÷2）=2，
故答案为：3，2．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
