题目内容
【题目】一个三角形可被剖成两个等腰三角形,原三角形的一个内角为36度,则原三角形最大内角的所有可能值为____________.
【答案】72°,90°,108°,132°,126°.
【解析】
分为以下情况:①原三角形是锐角三角形,最大角是72°的情况;②原三角形是直角三角形,最大角是90°的情况;③原三角形是钝角三角形,最大角是108°的情况;④原三角形是钝角三角形,最大角是126°的情况;⑤原三角形是钝角三角形,最大角是132°的情况.
解:①原三角形是锐角三角形,最大角是72°的情况如图所示: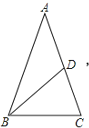
∠ABC=∠ACB=72°, ∠A=36°,AD=BD=BC;
②原三角形是直角三角形,最大角是90°的情况如图所示: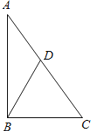
∠ABC=90°, ∠A=36°,AD=CD=BD;
③原三角形是钝角三角形,最大角是108°的情况如图所示: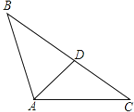
④原三角形是钝角三角形,最大角是126°的情况如图所示: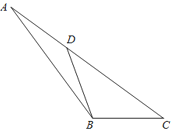
∠ABC=126°, ∠C=36°,AD=BD=BC;
⑤原三角形是钝角三角形,最大角是132°的情况如图所示: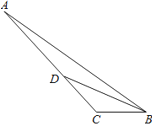
∠C=132°, ∠ABC=36°,AD=BD,CD=CB
综上,原三角形最大内角的所有可能值为72°,90°,108°,132°,126°.

练习册系列答案
相关题目