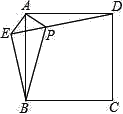
题目内容
【题目】如图,![]() 的四个内角的平分线分别相交于点
的四个内角的平分线分别相交于点![]() 、
、![]() 、
、![]() 、
、![]() ,四边形
,四边形![]() 是怎样的特殊四边形?证明你的结论.
是怎样的特殊四边形?证明你的结论.

【答案】矩形,证明见解析
【解析】
由于四边形ABCD是平行四边形,那么AB∥CD,利用平行线的性质可得∠ABC+∠BCD=180°,而BH,CH分别平分∠ABC与∠BCD,则∠HBC=![]() ∠ABC,∠HCB=
∠ABC,∠HCB=![]() ∠BCD,那么有∠HBC+∠HCB=90°,再利用三角形内角和定理可知∠H=90°,同理∠HEF=∠F=90°,利用三个内角等于90°的四边形是矩形,那么四边形EFGH是矩形.
∠BCD,那么有∠HBC+∠HCB=90°,再利用三角形内角和定理可知∠H=90°,同理∠HEF=∠F=90°,利用三个内角等于90°的四边形是矩形,那么四边形EFGH是矩形.
四边形EFGH是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵BH,CH分别平分∠ABC与∠BCD,
∴∠HBC=![]() ∠ABC,∠HCB=
∠ABC,∠HCB=![]() ∠BCD,
∠BCD,
∴∠HBC+∠HCB=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() ×180°=90°,
×180°=90°,
∴∠H=90°,
同理∠HEF=∠F=90°,
∴四边形EFGH是矩形.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目