Question

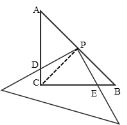
【题目】如图，在中，，，将一块等腰直角三角形的直角顶点放在斜边的中点处，将三角板绕点旋转，三角板的两直角边分别交射线、于、两点．如图①、②、③是旋转三角板得到的图形中的3种情况．

（1）观察图①，当三角板绕点旋转到时，我们发现：__________．（选填“”、“”或“”）

（2）当三角板绕点旋转到图②所示位置时，判断（1）题中与之间的大小关系还存在吗？请你结合图②说明理由．

（3）三角板绕点旋转，是否能成为等腰三角形？若能，指出所有情况（那写出为等腰三角形时的长）；若不能，请说明理由．

Answer 1

【答案】（1）=；（2）存在，PD＝PE，理由见解析；（3）能，当BE=0或6或6+或3时，为等腰三角形．

【解析】

（1）根据题意证明△ADP≌△BEP（AAS）即可解答；

（2）如图，连接PC，根据等腰三角形的性质得到∠ACP＝∠B＝∠BCP＝45°，BP＝CP，再根据等量代换得到∠DPC＝∠PBE，证明△DPC≌△PEB（ASA）即可；

（3）若△PCE是等腰三角形，需分三种情况进行讨论，①当PC＝PE＝时；②当PC＝CE＝时，E在线段BC上或点E在线段BC的延长线上；③当PE＝EC，根据等腰三角形的性质即可逐一解答．

解（1）当三角板绕点旋转到时，

∵∠ACB=DPE=90°，

∴∠PEB=90°，

∵AC=BC=6，

∴∠A=∠B=45°，

∵点P是AB的中点，

∴AP=BP，

∴△ADP≌△BEP（AAS）

∴PD=PE，

故答案为：=．

（2）存在，PD＝PE

如图，连接PC，

∵△ABC是等腰直角三角形，P是AB中点
∴CP⊥AB，∠ACP＝∠BCP＝∠ACB＝45°，
∴∠ACP＝∠B＝∠BCP＝45°
∴BP＝CP
∵∠DPC＋∠CPE＝90°，∠BPE＋∠CPE＝90°，
∴∠DPC＝∠PBE，

又∵BP＝CP，∠ACP＝∠B，
∴△DPC≌△PEB（ASA）
∴PD＝PE．

（3）能，

∵AC＝BC＝6，∠C＝90°
∴AB＝
∴AP＝BP＝CP＝，
若△PCE是等腰三角形
①当PC＝PE＝时，即B，E重合，BE＝0
②当PC＝CE＝时，E在线段BC上，则BE＝6，

E在线段BC的延长线上，则BE＝6＋，
③当PE＝EC，且∠PCB＝45°，
∴∠PEC＝90°，

∵PC=PB，

∴CE=BE=3，
综上所述，当BE=0或6或6+或3时，为等腰三角形．