题目内容
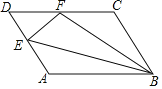
【题目】如图,在平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为12,△FCB的周长为28,则FC的长为_____.
【答案】8
【解析】
根据折叠的性质可得,EF=AE、BF=BA,从而平行四边形的周长可以转化为△FDE的周长+△FCB的周长,求出AB+BC,再由△FCB的周长28,即可求出FC的长.
由折叠的性质可得EF=AE、BF=AB,
∴平行四边形ABCD的周长
=DF+FC+CB+BA+AE+DE
=△FDE的周长+△FCB的周长
=12+28=40,
∵四边形ABCD为平行四边形
∴AB+BC=20,
∵△FCB的周长
=CF+BC+BF=CF+BC+AB=28
即FC+20=28
∴FC=8.
故答案为:8

练习册系列答案
相关题目