题目内容
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)
(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?

【答案】(1)5厘米;(2)当t为 ![]() 秒时,线段PQ将四边形ABCD的面积分为1:2两部分.
秒时,线段PQ将四边形ABCD的面积分为1:2两部分.
【解析】
(1)作DE⊥BC于E,则四边形ADEB是矩形,在直角△DEC中运用勾股定理即可求解;
(2)由题意可知BP=t厘米,则PC=(5﹣t)厘米,CQ=2t厘米,同时由题意可知0<t≤2.5;作QH⊥BC于点H,运用三角形相似可求解QH的长度表达式,则可列出△DEC的面积表达式,再按线段PQ将四边形ABCD的面积分为1:2两部分,分S△PQC:S四边形ABCD=1:3和S△PQC:S四边形ABCD=2:3两种情况分别讨论.
(1)解:如图1,作DE⊥BC于E,则四边形ADEB是矩形.
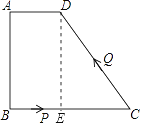
∴BE=AD=1,DE=AB=3,
∴EC=BC﹣BE=4,
在Rt△DEC中,DE2+EC2=DC2 ,
∴DC= ![]() =5厘米;
=5厘米;
(2)解:∵点P的速度为1厘米/秒,点Q的速度为2厘米/秒,运动时间为t秒,
∴BP=t厘米,PC=(5﹣t)厘米,CQ=2t厘米,QD=(5﹣2t)厘米,
且0<t≤2.5,
作QH⊥BC于点H,
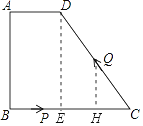
∴DE∥QH,
∴∠DEC=∠QHC,
∵∠C=∠C,
∴△DEC∽△QHC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴QH= ![]() t,
t,
∴S△PQC= ![]() PCQH=
PCQH= ![]() (5﹣t)
(5﹣t) ![]() t=﹣
t=﹣ ![]() t2+3t,
t2+3t,
S四边形ABCD= ![]() (AD+BC)AB=
(AD+BC)AB= ![]() (1+5)×3=9,
(1+5)×3=9,
分两种情况讨论:
①当S△PQC:S四边形ABCD=1:3时,
﹣ ![]() t2+3t=
t2+3t= ![]() ×9,即t2﹣5t+5=0,
×9,即t2﹣5t+5=0,
解得t1= ![]() ,t2=
,t2=![]() (舍去);
(舍去);
②S△PQC:S四边形ABCD=2:3时,
﹣ ![]() t2+3t=
t2+3t= ![]() ×9,即t2﹣5t+10=0,
×9,即t2﹣5t+10=0,
∵△<0,
∴方程无解,
∴当t为 ![]() 秒时,线段PQ将四边形ABCD的面积分为1:2两部分.
秒时,线段PQ将四边形ABCD的面积分为1:2两部分.