题目内容
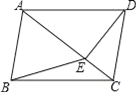
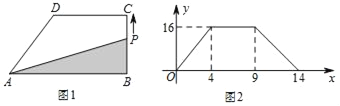
【题目】如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是 、 ;
(2)当点P运动的路程x=4时,△ABP的面积为y= ;
(3)求AB的长和梯形ABCD的面积.
【答案】(1)x,y;(2)16;(3)AB=8,梯形ABCD的面积=26.
【解析】
(1)依据点P运动的路程为x,△ABP的面积为y,即可得到自变量和因变量;
(2)依据函数图象,即可得到点P运动的路程x=4时,△ABP的面积;
(3)根据图象得出BC的长,以及此时三角形ABP面积,利用三角形面积公式求出AB的长即可;由函数图象得出DC的长,利用梯形面积公式求出梯形ABCD面积即可.
(1)∵点P运动的路程为x,△ABP的面积为y,∴自变量为x,因变量为y.
故答案为:x,y;
(2)由图可得:当点P运动的路程x=4时,△ABP的面积为y=16.
故答案为:16;
(3)根据图象得:BC=4,此时△ABP为16,∴![]() ABBC=16,即
ABBC=16,即![]() ×AB×4=16,解得:AB=8;
×AB×4=16,解得:AB=8;
由图象得:DC=9﹣4=5,则S梯形ABCD=![]() ×BC×(DC+AB)=
×BC×(DC+AB)=![]() ×4×(5+8)=26.
×4×(5+8)=26.

练习册系列答案
相关题目