题目内容
【题目】已知:![]() 平行线
平行线![]() 与
与![]() 与
与![]() 与
与![]() 之间的距离分别为
之间的距离分别为![]() 且
且![]()
![]() ,
,![]() .我们把四个顶点分别在
.我们把四个顶点分别在![]() 这四条平行线上的四边形称为“线上四边形”
这四条平行线上的四边形称为“线上四边形”
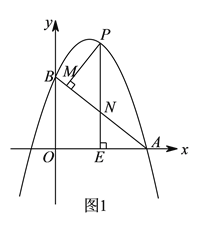
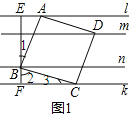
(1)如图1,正方形![]() 为“线上四边形”,
为“线上四边形”,![]() 于点
于点![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .求正方形
.求正方形![]() 的边长.
的边长.

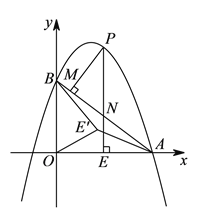
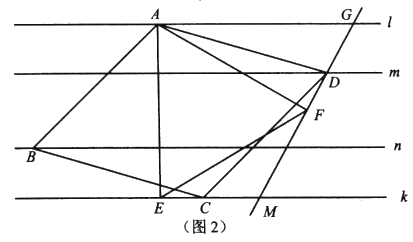
(2)如图2,菱形![]() 为“线上四边形”且
为“线上四边形”且![]() 是等边三角形,点
是等边三角形,点![]() 在直线
在直线![]() 上,连接
上,连接![]() 且
且![]() 的延长线分别交直线
的延长线分别交直线![]() 于点
于点![]() .求证:
.求证:![]() .
.
【答案】(1)![]() ;(2)见详解
;(2)见详解
【解析】
(1)利用AAS证明△ABE≌△BCF,即可求得AE和BE的长,然后利用勾股定理即可求解;
(2)先△ACE≌△ADF,然后利用全等的性质得到![]() .
.
解:(1)如图1,
∵BE⊥l,l∥k,
∴∠AEB=∠BFC=90°,
又四边形ABCD是正方形,
∴∠1+∠2=90°,AB=BC,∠2+∠3=90°,
∴∠1=∠3,
∴在△ABE和△BCF中,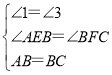 ,
,
∴△ABE≌△BCF(AAS),
∴AE=BF=2,
∵BE=d1+d2=2+3=5,
∴AB=![]() ,
,
∴正方形的边长是![]() ;
;
(2)如图,连接AC
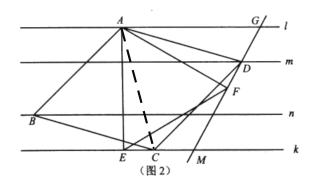
∵四边形ABCD是菱形
∴CD=AD
∵![]()
∴△ACD是等边三角形
∴AD=AC,∠CAD=60°
∵![]() 是等边三角形
是等边三角形
∴AE=AF,∠EAF=60°
∵∠FAD=∠CAD-∠CAF =60°-∠CAF
∠EAC=∠EAF-∠CAF =60°-∠CAF
∴∠FAD=∠EAC
∴在△ACE和△ADF中,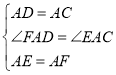 ,
,
∴△ACE≌△ADF(SAS),
∴![]() .
.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目