题目内容
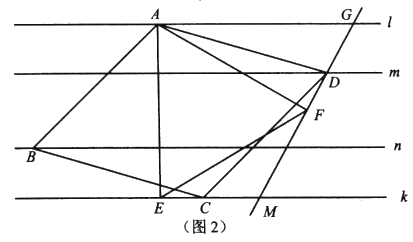
【题目】如图,AB是半圆半径,半径OC⊥AB于点O,点D是弧BC的中点,连接CD、AD、OD,给出以下四个结论:①∠DOB=∠ADC;②CE=OE;③△ODE∽△ADO;④2CD2=CE·AB.其中正确结论的序号是( )

A. ①③ B. ②④ C. ①④ D. ①②③
【答案】C
【解析】试题分析:①∵AB是半圆直径,∴AO=OD,∴∠OAD=∠ADO,∵AD平分∠CAB交弧BC于点D, ∴∠CAD=∠DAO=![]() ∠CAB, ∴∠CAD=∠ADO, ∴AC∥OD,
∠CAB, ∴∠CAD=∠ADO, ∴AC∥OD,
∴∠DOB=∠CAO,又∵∠CAO=∠ADC(都对着半圆弧),∴∠DOB=∠ADC故①正确;
②由题意得,OD=R,AC=![]() R, ∵OE:CE=OD:AC=1:
R, ∵OE:CE=OD:AC=1: ![]() ,
,
∴OE≠CE,故②错误;
③∵在△ODE和△ADO中,只有∠ADO=∠EDO,∵∠COD=2∠CAD=2∠OAD,
∴∠DEO≠∠DAO,∴不能证明△ODE和△ADO相似, ∴③错误;
④∵AD平分∠CAB交弧BC于点D,∴∠CAD=![]() ×45°=22.5°,
×45°=22.5°,
∴∠COD=45°, ∵AB是半圆直径,∴OC=OD, ∴∠OCD=∠ODC=67.5°
∵∠CAD=∠ADO=22.5°(已证), ∴∠CDE=∠ODC-∠ADO=67.5°-22.5°=45°,
∴△CED∽△COD, ∴![]() , ∴
, ∴![]() =
= ![]() , ∴
, ∴![]() .
.
∴④正确.故选C.

【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:

学生最喜欢的节目人数条形统计图
节目 | 人数( 名 ) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 |
|
中国诗词大会 |
| 40% |
出彩中国人 | 10 | 20% |
学生最喜爱的节目人数统计表
根据以上提供的信息,解答下列问题:
(1)![]() =
= ![]() =
= ![]() = ;
= ;
(2)补全条形统计图;
(3)若该校共有学生1200名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名?