题目内容
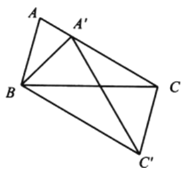
【题目】如图,在![]() 中,
中,![]() ,以点
,以点![]() 为旋转中心把
为旋转中心把![]() 按顺时针旋转一定角度,得到
按顺时针旋转一定角度,得到![]() 点
点![]() 恰好落在
恰好落在![]() 上,连接
上,连接![]() 则
则![]() 度数为( )
度数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
在△ABC中,可求得∠ABC和∠ACB,在△ABA′中由旋转的性质可求得∠ABA′的大小,从而可求得∠CBC′,在△BCC′中可求得∠BCC′,从而可求得∠ACC′
解:
∵AC=BC,
∴∠A=∠ABC=70°,
∴∠ACB=180°-∠A-∠ABC =180°-70°-70°=40°,
∵以点B为旋转中心把△ABC按顺时针旋转,得到△A′BC′,
∴AB=A′B,BC=BC′,且∠CBC′=∠ABA′,
∴∠BA′A=∠A=70°,
∴∠ABA′=40°,
∴∠CBC′=40°,
∴∠BCC′=![]() =70°,
=70°,
∴∠ACC′=∠ACB+∠BCC′=40°+70°=110°.
故选A.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目