题目内容
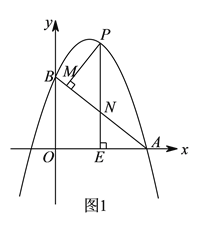
【题目】如图![]() ,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(![]() )分别求出直线AB和抛物线的函数表达式;
)分别求出直线AB和抛物线的函数表达式;
(![]() )设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
(![]() )如图2,在(
)如图2,在(![]() )条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
)条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
①在x轴上找一点Q,使△OQE'∽△OE'A,并求出Q点的坐标;
②求BE'+![]() AE'的最小值.
AE'的最小值.
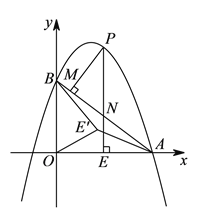
【答案】(1)![]() ;
; ![]() ;(2)4;(3)①
;(2)4;(3)①![]() ,②
,②![]() .
.
【解析】分析:(1)把点A(8,0)代入抛物线y=ax-6ax+6,可求得a的值,从而可得到抛物线的解析式,然后求得点A和点B的坐标,最后利用待定系数法可求得直线AB的解析式;
(2)E(m,0),则N(m,-![]() m+6),P(m,
m+6),P(m, ![]() +6),然后证明△ANE∽△ABO,依据相似三角形的性质可求得AN的长,接下来,再证明△NMP∽△NEA,然后依据相似三角形的性质可得到
+6),然后证明△ANE∽△ABO,依据相似三角形的性质可求得AN的长,接下来,再证明△NMP∽△NEA,然后依据相似三角形的性质可得到![]() ,从而可求得PM=12-
,从而可求得PM=12-![]() m,然后依据PM=
m,然后依据PM=![]() m+3m,然后列出关于m的方程求解即可;
m+3m,然后列出关于m的方程求解即可;
(3)①在(2)的条件下,m=4,则OE′=OE=4,然后再证明△OQE′∽△OE′A,依据相似三角形的性质可得到![]() ,从而可求得OQ的值,于是可得到点Q的坐标;
,从而可求得OQ的值,于是可得到点Q的坐标;
②由①可知,当Q为(2,0)时,△OQE′∽△OE′A,且相似比为![]() ,于是得到BE′+
,于是得到BE′+![]() AE′=BE′+QE′,当点B、Q、E′在一条直线上时,BE′+QE′最小,最小值为BQ的长.
AE′=BE′+QE′,当点B、Q、E′在一条直线上时,BE′+QE′最小,最小值为BQ的长.
本题解析:
(![]() )把点
)把点![]() 代入抛物线
代入抛物线![]()
得![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() 与
与![]() 轴交点,令
轴交点,令![]() ,
,
得![]() ,
,
∴![]() .
.
设![]() 为
为![]() 过
过![]() ,
, ![]() ,
,
∴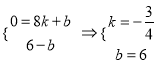 ,
,
∴![]() .
.
(![]() )∵过
)∵过![]() 作
作![]() 轴垂线交
轴垂线交![]() 于
于![]() ,交抛物线于
,交抛物线于![]() ,
,
∵![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴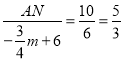 ,
,
∴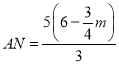 ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴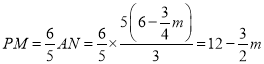 ,
,
∵![]() ,
,
∴![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() .
.
(![]() )①在(
)①在(![]() )的条件下,
)的条件下, ![]() ,∴
,∴![]() ,
,
设![]() ,∵旋转,∴
,∵旋转,∴![]() ,
,
若![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
②由①可知,当![]() 为
为![]() 时,
时,
![]() ,且相似比为
,且相似比为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() 旋转到
旋转到![]() 所在直线上时,
所在直线上时, ![]() 最小,即为
最小,即为![]() 长度,
长度,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.