题目内容
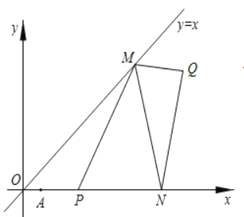
【题目】平面直角坐标系中,直线![]() ,点
,点![]() ,点
,点![]() ,动点
,动点![]() 在直线
在直线![]() 上,动点
上,动点![]() 、
、![]() 在
在![]() 轴正半轴上,连接
轴正半轴上,连接![]() 、
、![]() 、
、![]() .
.
(1)若点![]() ,求直线
,求直线![]() 的解析式;
的解析式;
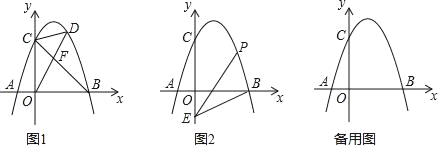
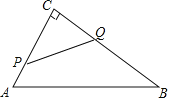
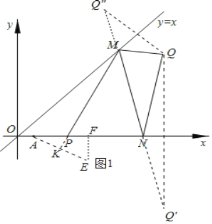
(2)如图![]() ,当
,当![]() 周长最小时,连接
周长最小时,连接![]() ,求
,求![]() 的最小值,并求出此时点
的最小值,并求出此时点![]() 的坐标;
的坐标;
【答案】(1)![]() ;(2)最小值为
;(2)最小值为![]() ;P点坐标为
;P点坐标为![]() .
.
【解析】
(1)设直线![]() 的解析式为
的解析式为![]() ,根据点M、Q的坐标,利用待定系数法求出k、b的值即可得答案;(2)作点
,根据点M、Q的坐标,利用待定系数法求出k、b的值即可得答案;(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 连接
连接![]() 交
交![]() 轴于
轴于![]() ,交直线
,交直线![]() 于
于![]() ,此时
,此时![]() 周长最小,根据题意可得点
周长最小,根据题意可得点![]() 和
和![]() 的坐标,即可求出直线
的坐标,即可求出直线![]() 的解析式,联立y=x,即可求出M点坐标,点
的解析式,联立y=x,即可求出M点坐标,点![]() ,作
,作![]() 于
于![]() ,作
,作![]() 于
于![]() ,则
,则![]() ,
,![]() ,
,![]() ,根据∠EAF的正弦值可得
,根据∠EAF的正弦值可得![]() ,根据垂线段最短可知,
,根据垂线段最短可知,![]() 、
、![]() 、
、![]() 共线时,
共线时,![]() 的值最小,可得
的值最小,可得![]() ,进而可得直线AE和MK的解析式,联立两个解析式即可求出K点坐标,根据两点距离公式即可求出MK和MQ的值,即可得答案.
,进而可得直线AE和MK的解析式,联立两个解析式即可求出K点坐标,根据两点距离公式即可求出MK和MQ的值,即可得答案.
(1)设直线![]() 的解析式为
的解析式为![]() ,
,
则有![]() ,
,
解得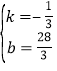 ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
(2)如图![]() 中,作点
中,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 连接
连接![]() 交
交![]() 轴于
轴于![]() ,交直线
,交直线![]() 于
于![]() ,此时
,此时![]() 周长最小.
周长最小.
由题意![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
由![]() ,解得
,解得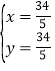 ,
,
![]() ,
,
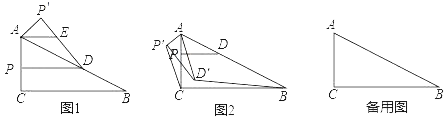
取点![]() ,作
,作![]() 于
于![]() ,作
,作![]() 于
于![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
根据垂线段最短可知,当![]() 、
、![]() 、
、![]() 共线时,
共线时,![]() 的值最小,
的值最小,
∵![]() ,
,![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
设直线MK的解析式为y=kx+b,
![]() ,
,
∴k=![]() ,
,
把M点坐标代入得:![]() =
=![]() ×
×![]() +b,
+b,
解得:b=![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
当y=0时,![]() =0,
=0,
解得:x=![]() ,
,
∴P点坐标为(![]() ,0).
,0).
由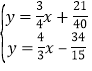 ,解得
,解得 ,
,
![]() ,
,
∴MK=![]() =
=![]() ,
,
MQ=![]() =
=![]()
∴![]() 的最小值
的最小值![]() .此时点
.此时点![]() 的坐标为
的坐标为![]() .
.

【题目】电影公司随机收集了2000部电影的有关数据,经分类整理得到如表:
电影类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 | 第六类 |
电影部数 | 140 | 50 | 300 | 200 | 800 | 510 |
好评率 |
|
|
|
|
|
|
注:好评率是指一类电影中获得好评的部数与该类电影的部数的比值.
![]() 如果电影公司从收集的电影中随机选取1部,那么抽到的这部电影是获得好评的第四类电影的概率是______;
如果电影公司从收集的电影中随机选取1部,那么抽到的这部电影是获得好评的第四类电影的概率是______;
![]() 电影公司为了增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化
电影公司为了增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化![]() 假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加
假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加![]() ,哪类电影的好评率减少
,哪类电影的好评率减少![]() ,可使改变投资策略后总的好评率达到最大?
,可使改变投资策略后总的好评率达到最大?
答:______.