题目内容
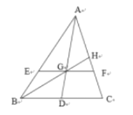
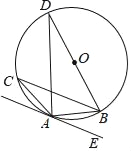
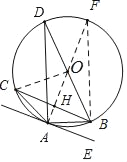
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2,求AD的长.
,AC=2,求AD的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据题目中已出现切点可确定用“连半径,证垂直”的方法证明切线,连接AO并延长交⊙O于点F,连接BF,则AF为直径,∠ABF=90°,根据同弧所对的圆周角相等,则可得到∠BAE=∠F,既而得到AE与⊙O相切于点A.
(2))连接OC,先由平行和已知可得∠ACB=∠ABC,所以AC=AB,则∠AOC=∠AOB,从而利用垂径定理可得AH=1,在Rt△OBH中,设OB=r,利用勾股定理解得r=2,在Rt△ABD中,即可求得AD的长为2![]() .
.
解:(1)连接AO并延长交⊙O于点F,连接BF,
则AF为直径,∠ABF=90°,
∵![]() ,
,
∴∠ACB=∠F,
∵∠BAE=∠ACB,
∴∠BAE=∠F,
∵∠FAB+∠F=90°,
∴∠FAB+∠BAE=90°,
∴OA⊥AE,
∴AE与⊙O相切于点A.
(2)连接OC,
∵AE∥BC,
∴∠BAE=∠ABC,
∵∠BAE=∠ACB,
∴∠ACB=∠ABC,
∴AC=AB=2,
∴∠AOC=∠AOB,
∵OC=OB,
∴OA⊥BC,
∴CH=BH=![]() BC=
BC=![]() ,
,
在Rt△ABH中,
AH=![]() =1,
=1,
在Rt△OBH中,设OB=r,
∵OH2+BH2=OB2,
∴(r﹣1)2+(![]() )2=r2,
)2=r2,
解得:r=2,
∴DB=2r=4,
在Rt△ABD中,AD=![]() =
=![]() =2
=2![]() ,
,
∴AD的长为2![]() .
.

练习册系列答案
相关题目