题目内容
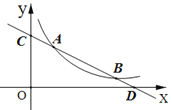
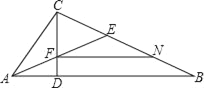
【题目】如图，抛物线y＝ax2+2x+c（a＜0）与x轴交于点A和点B（点A在原点的左侧，点B在原点的右侧），与y轴交于点C，OB＝OC＝3．
(1)求该抛物线的函数解析式．
(2)如图1，连接BC，点D是直线BC上方抛物线上的点，连接OD，CD．OD交BC于点F，当S△COF：S△CDF＝3：2时，求点D的坐标．
(3)如图2，点E的坐标为（0，
），点P是抛物线上的点，连接EB，PB，PE形成的△PBE中，是否存在点P，使∠PBE或∠PEB等于2∠OBE？若存在，请直接写出符合条件的点P的坐标；若不存在，请说明理由．
【答案】(1)y＝﹣x2+2x+3；(2)点D的坐标为（1，4）或（2，3）；(3)点P坐标为：（
，
）或（
，
）．
【解析】
（1）OB=OC=3，则：B（3，0），C（0，-3），把B、C坐标代入抛物线方程，解得抛物线方程为：y=-x2+2x+3；
（2）S△COF：S△CDF=3：2，则S△COF=
S△COD，即：xD=xF，即可求解；
（3）分∠PBE或∠PEB等于2∠OBE两种情况分别求解即可．
(1)OB＝OC＝3，则：B（3，0），C（0，﹣3），
把B、C坐标代入抛物线方程，
解得抛物线方程为：y＝﹣x2+2x+3；
(2)∵S△COF：S△CDF＝3：2，
∴S△COF＝S△COD，即：xD＝xF，
设：F点横坐标为3t，则D点横坐标为5t，
点F在直线BC上，
而BC所在的直线方程为：y＝﹣x+3，则F（3t，3﹣3t），
则：直线OF所在的直线方程为：y＝
x＝
x，
则点D（5t，5﹣5t），
把D点坐标代入①，解得：t＝
或
，
则点D的坐标为（1，4）或（2，3）；
(3)①如图所示，当∠PEB＝2∠OBE＝2α时，
过点E作∠PEB的平分线交x轴于G点，PE交x轴于H点，
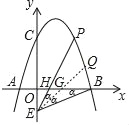
则：∠PEQ＝∠QEB＝∠ABE＝α，则∠HGE＝2α，
设：GB＝m，则：OG＝3﹣m，GE＝m，
在Rt△OGE中，由勾股定理得：EG2＝OG2+OE2，
即：m2＝（3﹣m）2+（
）2，解得：m＝
，
则：GE＝，OG＝
，BE＝
，
∵∠PEQ＝∠ABE＝α，∠EHG＝∠EHG，∴△HGE∽△HEB，
∴
＝
＝
，设：GH＝
x，HE＝4x，
在Rt△OHE中，OH＝OG﹣HG＝﹣x，OE＝，EH＝4x，
由勾股定理解得：x＝
，则：OH＝
，H（，0），
把E、H两点坐标代入一次函数表达式，
解得EH所在直线的表达式为：y＝
x﹣，
将上式与①联立并解得：x＝，
则点P（，）；
②当∠PBE＝2∠OBE时，则∠PBO＝∠EBO，
BE所在直线的k值为
，则BE所在直线的k值为﹣，
则：PB所在的直线方程为：y＝﹣x+3，
将上式与①联立，解得：x＝，（x＝0已舍去），
则点P（，），
故：点P坐标为：（，）或（，）．
