题目内容
【题目】如图,在![]() 中,
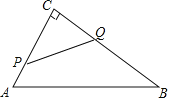
中,![]() ,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止)。则四边形PABQ的面积y(
,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止)。则四边形PABQ的面积y(![]() )与运动时间x(s)之间的函数图象为( )
)与运动时间x(s)之间的函数图象为( )
A. 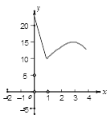 B.
B. 
C. 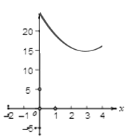 D.
D. 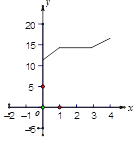
【答案】C
【解析】
在Rt△ABC中,利用勾股定理可得出AC=6cm,设运动时间为x(0≤x≤4),则PC=(6-x)cm,CQ=2xcm,利用分割图形求面积法可得出S四边形PABQ=x2-6x+24,根据函数解析式可得函数图象为抛物线即可得答案.
解:在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,
∴AC=![]() =6cm,
=6cm,
设运动时间为x(0≤x≤4),则PC=(6-x)cm,CQ=2xcm,
∴S四边形PABQ=S△ABC-S△CPQ
=![]() ACBC-
ACBC-![]() PCCQ
PCCQ
=![]() ×6×8-
×6×8-![]() ×(6-x)×2x
×(6-x)×2x
=x2-6x+24
=(x-3)2+15.
根据函数解析式可得函数图象应为:C.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目