题目内容
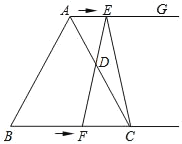
【题目】如图,在ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE=![]() ∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是_____.
∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是_____.

【答案】①②③
【解析】
根据平行四边形的性质可得![]() ,再证明
,再证明![]() 是等腰三角形,根据等腰三角形的性质可得
是等腰三角形,根据等腰三角形的性质可得![]() ,进而得到
,进而得到![]() ;首先证明
;首先证明![]() ,再根据三角形中位线的性质可得
,再根据三角形中位线的性质可得![]() ,进而得到
,进而得到![]() ;证明
;证明![]() ,根据平行线的性质可得
,根据平行线的性质可得![]() ,再根据等边对等角可得
,再根据等边对等角可得![]() ,进而得到
,进而得到![]() .
.
①∵四边形ABCD是平行四边形,
∴![]()
∴![]()
∵![]() ,
,
∴![]()
∴![]()
∵E是CO中点![]()
∴![]()
∴![]()
故①正确;
②∵![]()
∴![]() 是等腰三角形,
是等腰三角形,
∵E是CO中点,
∴![]() ,
,
∴![]() ,
,
∵G为AB中点,
∴![]() ,
,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E、F分别OC、OD是的中点,
∴![]() ,
,
∴![]() ,
,
故②正确;
③∵E、F分别OC、OD是的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ∠EFG=∠AGF,
∠EFG=∠AGF,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴GF平分![]() ,
,
故③正确;
④在![]() 中
中
∵G为AB的中点,
而BE与AE不一定相等,
∴EG与AB不一定垂直,
∵![]()
∴EF与GE不一定垂直,
故④错误;
综上:①②③正确,
故答案是:①②③

练习册系列答案
相关题目