ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§‘ΎΒ»±Ώ»ΐΫ«–ΈABC÷–Θ§BCΘΫ8cmΘ§…δœΏAGΓΈBCΘ§ΒψE¥”ΒψA≥ωΖΔ―Ί…δœΏAG“‘1cm/sΒΡΥΌΕ»‘ΥΕ·Θ§Ά§ ±ΒψF¥”ΒψB≥ωΖΔ―Ί…δœΏBC“‘2cm/sΒΡΥΌΕ»‘ΥΕ·Θ§…η‘ΥΕ· ±ΦδΈΣtΘ®sΘ©Θ°
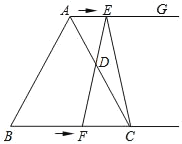
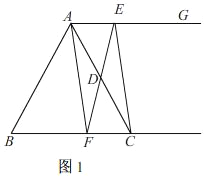
Θ®1Θ©Ν§Ϋ”EFΘ§Β±EFΨ≠ΙΐAC±ΏΒΡ÷–ΒψD ±Θ§«σ÷ΛΘΚΥΡ±Ώ–ΈAFCE «ΤΫ––ΥΡ±Ώ–ΈΘΜ
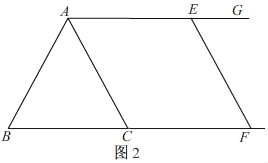
Θ®2Θ©ΧνΩ’ΘΚΔΌΒ±tΈΣΓΓ ΓΓs ±Θ§ΥΡ±Ώ–ΈACFE «Νβ–ΈΘΜΔΎΒ±tΈΣΓΓ ΓΓs ±Θ§ΓςACEΒΡΟφΜΐ «ΓςACFΒΡΟφΜΐΒΡ2±ΕΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘΜ
Θ®2Θ©ΔΌ8ΘΜΔΎt=![]() Μρy=
Μρy=![]() .
.
ΓΨΫβΈωΓΩ
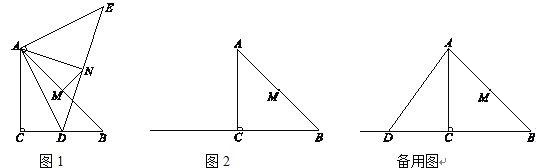
Θ®1Θ©≈–Εœ≥ωΓςADEΓ’ΓςCDFΒΟ≥ωAEΘΫCFΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©ΔΌœ»«σ≥ωACΘΫBCΘΫ8Θ§ΫχΕχ≈–Εœ≥ωAEΘΫCFΘΫACΘΫ8Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
ΔΎœ»≈–Εœ≥ωΓςACEΚΆΓςACFΒΡ±ΏAEΚΆCF…œΒΡΗΏœύΒ»Θ§ΫχΕχ≈–Εœ≥ωAEΘΫ2CFΘ§‘ΌΖ÷ΝΫ÷÷«ιΩωΘ§Ϋ®ΝΔΖΫ≥Χ«σΫβΦ¥Ω…ΒΟ≥ωΫα¬έΘ°
ΫβΘΚΘ®1Θ©»γΆΦ1Θ°
ÿAGøBCȧ
ΓύΓœEAC=ΓœFCAΘ§ΓœAED=ΓœCFDΘ°
ΓΏEFΨ≠ΙΐAC±ΏΒΡ÷–ΒψDΘ§
ΓύAD=CDΘ§
ΓύΓςADEΓ’ΓςCDFΘ®AASΘ©Θ§
ΓύAE=CFΘ°
ÿAEøFCȧ
ΓύΥΡ±Ώ–ΈAFCE «ΤΫ––ΥΡ±Ώ–ΈΘΜ
Θ®2Θ©ΔΌ»γΆΦ2Θ°
ΓΏΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύAC=BC=8Θ°
ΓΏΥΡ±Ώ–ΈACFE «Νβ–ΈΘ§
ΓύAE=CF=AC=BC=8Θ§«“ΒψF‘ΎBC―”≥ΛœΏ…œΘ§”…‘ΥΕ·÷ΣΘ§AE=tΘ§BF=2tΘ§
ΓύCF=2t©¹8Θ§t=8Θ§ΫΪt=8¥ζ»κCF=2t©¹8÷–Θ§
ΒΟCF=8=AC=AEΘ§ΖϊΚœΧβ“βΘ§Φ¥ΘΚt=8Οκ ±Θ§ΥΡ±Ώ–ΈACFE «Νβ–ΈΘ°
Ι ¥πΑΗΈΣΘΚ8ΘΜ
ΔΎ…ηΤΫ––œΏAG”κBCΒΡΨύάκΈΣhΘ§
ΓύΓςACE±ΏAE…œΒΡΗΏΈΣhΘ§ΓςACFΒΡ±ΏCF…œΒΡΗΏΈΣhΘ°
ΓΏΓςACEΒΡΟφΜΐ «ΓςACFΒΡΟφΜΐΒΡ2±ΕΘ§
ΓύAE=2CFΘ§Β±ΒψF‘ΎœΏΕΈBC…œ ±Θ®0ΘΦtΘΦ4Θ©Θ§CF=8©¹2tΘ§AE=tΘ§
Γύt=2Θ®8©¹2tΘ©Θ§
Γύ![]()
Β±ΒψF‘ΎBCΒΡ―”≥ΛœΏ…œ ±Θ®tΘΨ4Θ©Θ§CF=2t©¹8Θ§AE=tΘ§
Γύt=2Θ®2t©¹8Θ©Θ§
Γύ![]()
Φ¥ΘΚt=![]() ΟκΜρ
ΟκΜρ![]() Οκ ±Θ§ΓςACEΒΡΟφΜΐ «ΓςACFΒΡΟφΜΐΒΡ2±ΕΘ°
Οκ ±Θ§ΓςACEΒΡΟφΜΐ «ΓςACFΒΡΟφΜΐΒΡ2±ΕΘ°
Ι ¥πΑΗΈΣΘΚ![]() Μρ
Μρ![]() Θ°
Θ°

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ