Question

【题目】探究与发现：

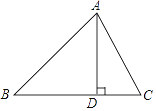
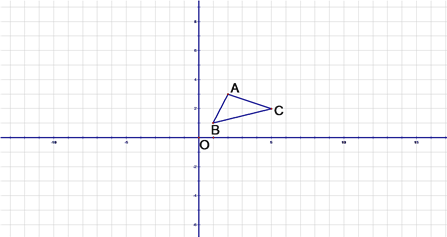
如图1所示的图形，像我们常见的学习用品--圆规．我们不妨把这种图形叫做“规形图”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？请解决以下问题：

(1)观察“规形图”，试探究∠BPC与∠A、∠B、∠C之间的关系，并说明理由；

(2)请你直接利用以上结论，解决以下问题：

①如图2：已知△ABC，BP平分∠ABC，CP平分∠ACB，直接写出∠BPC与∠A之间存在的等量关系为： ．

迁移运用：如图3：在△ABC中，∠A=80°，点O是∠ABC，∠ACB角平分线的交点，点P是∠BOC，∠OCB角平分线的交点，若∠OPC=100°，则∠ACB的度数 ．

②如图4：若D点是△ABC内任意一点，BP平分∠ABD，CP平分∠ACD．直接写出∠BDC、∠BPC、∠A之间存在的等量关系为 ．

Answer 1

【答案】(1)∠BPC=∠A+∠B+∠C，理由见解析；(2)①∠BPC=90°+∠A，60°；②2∠BPC=∠BDC+∠A．

【解析】

（1）首先连接AP并延长至点F，然后根据外角的性质，即可判断出∠BPC=∠A+∠B+∠C；

（2）①利用角平分线的定义，三角形的内角和定理证明即可；

迁移运用：设∠BCP=∠PCO=x，∠BOP=∠COP=y，由∠P=100°，推出x+y=80°，推出2x+2y=160°，推出∠OBC=180°-160°=20°，可得∠ABC=40°，由此即可解决问题；

②根据角平分线的定义和四边形的内角和即可得到结论．

(1)如图，连接AP并延长至点F，

根据外角的性质，可得

∠BPF=∠BAP+∠B，∠CPF=∠C+∠CAP，

又∵∠BPC=∠BPF+∠CPF，∠BAC=∠BAP+∠CAP，

∴∠BPC=∠A+∠B+∠C；

(2)①结论：∠BPC=90°+∠A．

理由：∵BP平分∠ABC，CP平分∠ACB，

∴∠PBC=∠ABC，∠PCB=∠ACB，

∴∠BPC=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+∠A；

迁移运用：设∠BCP=∠PCO=x，∠BOP=∠COP=y，

∵∠P=100°，

∴x+y=80°，

∴2x+2y=160°，

∴∠OBC=180°-160°=20°，

∵BO平分∠ABC，

∴∠ABC=40°，

∵∠A=80°，

∴∠ACB=180°-40°-80°=60°；

故答案为：∠BPC=90°+∠A，60°；

②∵BP平分∠ABD，CP平分∠ACD，

∴∠PBD=∠ABP，∠PCD=∠ACP，

四边形BPDC中，∠P+∠ABD+∠ACD+360°-∠D=360°，

∴∠ABD+∠ACD=∠D-∠P，

在四边形ABPC中，∠A+∠ABD+∠ACD+360°-∠P=360°，

∴∠A+∠D-∠P-∠P=0，

∴2∠BPC=∠BDC+∠A．

故答案为：2∠BPC=∠BDC+∠A．