��Ŀ����
ij��������һ��ÿ������Ϊ40Ԫ��С�ҵ�,���г�����Ԥ��,�ۼ۶�Ϊ50Ԫʱ���۳�400��������ÿ����1Ԫ,������������10��.
��1����ÿ����������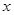 Ԫ,��ʱ���������Ƕ��٣����ú�
Ԫ,��ʱ���������Ƕ��٣����ú�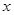 �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2�����������������6000Ԫ,����ʹ����������,��ÿ��Ӧ����Ϊ����Ԫ��
��3��������Ҫ����������,��ÿ��Ӧ���۶���Ԫ?��õ���������Ƕ��٣�
��1����ÿ����������
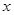 Ԫ,��ʱ���������Ƕ��٣����ú�
Ԫ,��ʱ���������Ƕ��٣����ú�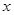 �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ����2�����������������6000Ԫ,����ʹ����������,��ÿ��Ӧ����Ϊ����Ԫ��
��3��������Ҫ����������,��ÿ��Ӧ���۶���Ԫ?��õ���������Ƕ��٣�
��1��50+x��40=x+10��Ԫ����
��2��Ҫʹ����������,��ÿ������Ϊ70Ԫ,Ӧ����200����
��3��ÿ������Ϊ65Ԫʱ���������,�ɻ�õ����������6250Ԫ��
��2��Ҫʹ����������,��ÿ������Ϊ70Ԫ,Ӧ����200����
��3��ÿ������Ϊ65Ԫʱ���������,�ɻ�õ����������6250Ԫ��
�����������1����������=���ۼ۩������й�ϵʽ��
��2��������=ÿ���������������,������Ϊ400��10x,�з������,��������ȡ�
��3�����ú�������������ֵ��
���������������ã�
��1��50+x��40=x+10��Ԫ����
��2����ÿ����������xԪ��
�г�����Ϊ����x+10����400��10x��=6000��
��ã�x1="10" , x2=20��
Ҫʹ����������,��ÿ������Ϊ70Ԫ,Ӧ����200����
��3����ÿ����������xԪ,�������ΪyԪ��
y=��x+10����400��10x��=��10x2+300x+4000=��10��x��15��2+6250
��x=15ʱ,y�����ֵΪ6250��
����ÿ������Ϊ65Ԫʱ���������,�ɻ�õ����������6250Ԫ��

��ϰ��ϵ�д�
 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
�����Ŀ
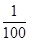 x��150,�ɱ�Ϊ20Ԫ/��,������ΪW����Ԫ��;����ֻ�ڹ�������,���ۼ۸�Ϊ150Ԫ/��,�ܸ��ֲ�ȷ������Ӱ��,�ɱ�ΪaԪ/����aΪ����,10��a��40��,��������Ϊx������ʱ,ÿ�»������
x��150,�ɱ�Ϊ20Ԫ/��,������ΪW����Ԫ��;����ֻ�ڹ�������,���ۼ۸�Ϊ150Ԫ/��,�ܸ��ֲ�ȷ������Ӱ��,�ɱ�ΪaԪ/����aΪ����,10��a��40��,��������Ϊx������ʱ,ÿ�»������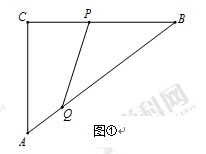
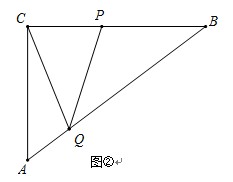
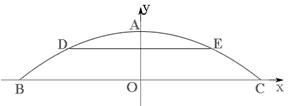
 �������۹��������۵��۲����ڳɱ��ۣ���ÿ���������ڳɱ��۵�60%��
�������۹��������۵��۲����ڳɱ��ۣ���ÿ���������ڳɱ��۵�60%�� ��ͼ���ϣ���x2��x1��m����y2��y1,��m��ȡֵ��ΧΪ ��
��ͼ���ϣ���x2��x1��m����y2��y1,��m��ȡֵ��ΧΪ �� Rt
Rt ��
�� ����ֱ�DZ���������
����ֱ�DZ��������� �ı߳���Ϊ2����
�ı߳���Ϊ2���� ��
�� ��ͬһֱ���ϣ���ʼʱ��
��ͬһֱ���ϣ���ʼʱ�� ���
��� �غϣ���
�غϣ��� ���
��� �غ�Ϊֹ����
�غ�Ϊֹ���� �ij�Ϊ
�ij�Ϊ ��
�� ����
����
